現在このページは書き途中で、更新・訂正されることがあります。足りない点などもあると思いますがご了承ください。

算数・数学教育の考え方

ここでは算数・数学教育の考え方についてまとめます。

偏差値160の勉強法について

子供が数学を最大8学年先取りし、全国統一中学生テストの数学（難関）では偏差値163.7を記録しました。ここではそんな我が家の算数・数学の勉強法をまとめていきます。

算数・数学教育の考え方の基本と流れ

我が家では算数と数学を区別せず、また学年ごとにも分けず、幼少期から大学まで繋がっている1つのものとして考えました。

中学受験はその大きな流れの途中にある1イベントとして、その時は対策に時間を充てますが、それ以外の時は学年は気にせず興味と効率を優先して学んでいく、という感じです。

進度と難度

算数・数学全体のフィールドを考える際は、進度と難度という2つの軸で捉えました。

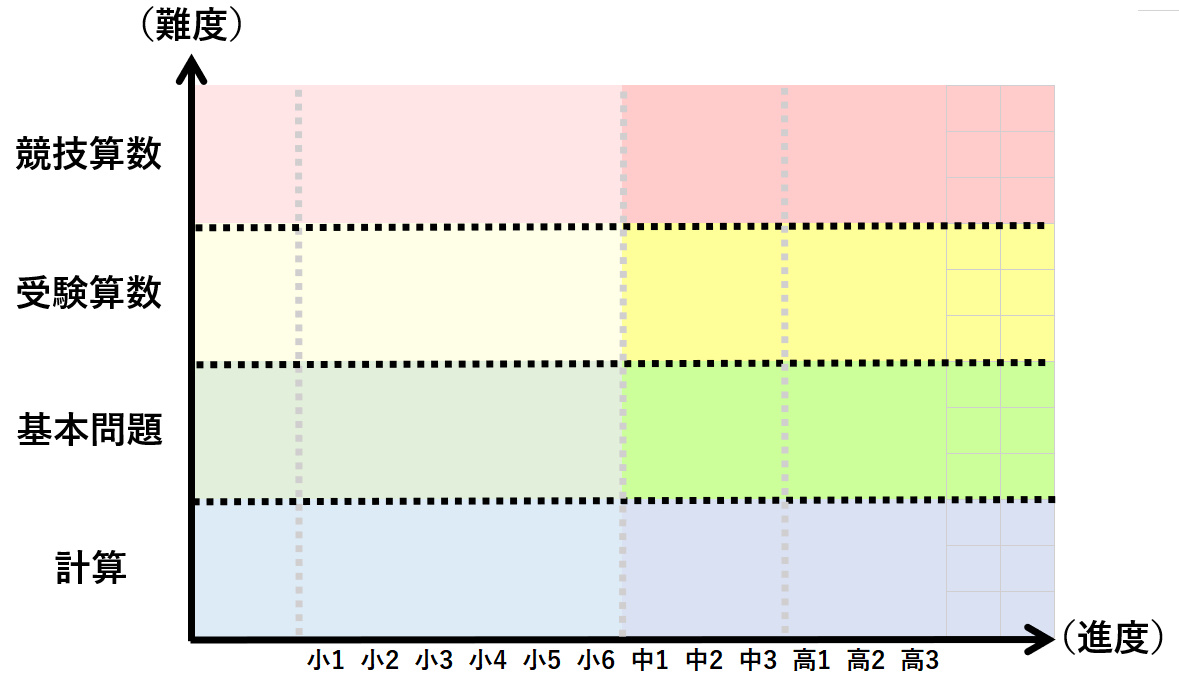
これは筆者の独自の考え方なので、少し説明します。

横軸の進度とは、本来学校で習う学年を表します。例えば「分数」「割合」「比」など新しい単元を学ぶ場合は、右に進むことになります。

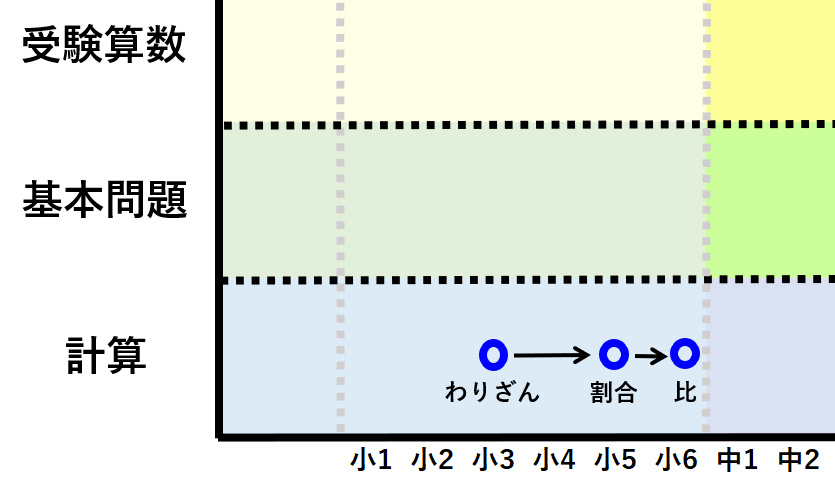
そして縦軸は難度です。例えば「比」を覚えた後に、基本問題をこなし、「比を使った旅人算」を学ぶ場合は、上に進むわけです。

この概念を用いて、現在どの学年の内容をどの難度まで習得できているかを把握しました。

ポイント秩序立っていない順番で早期教育を行うと、しばしば基本をやっていない単元の応用問題に出くわしてしまうものですが、この表ではそのことも可視化できます。

目標の設定

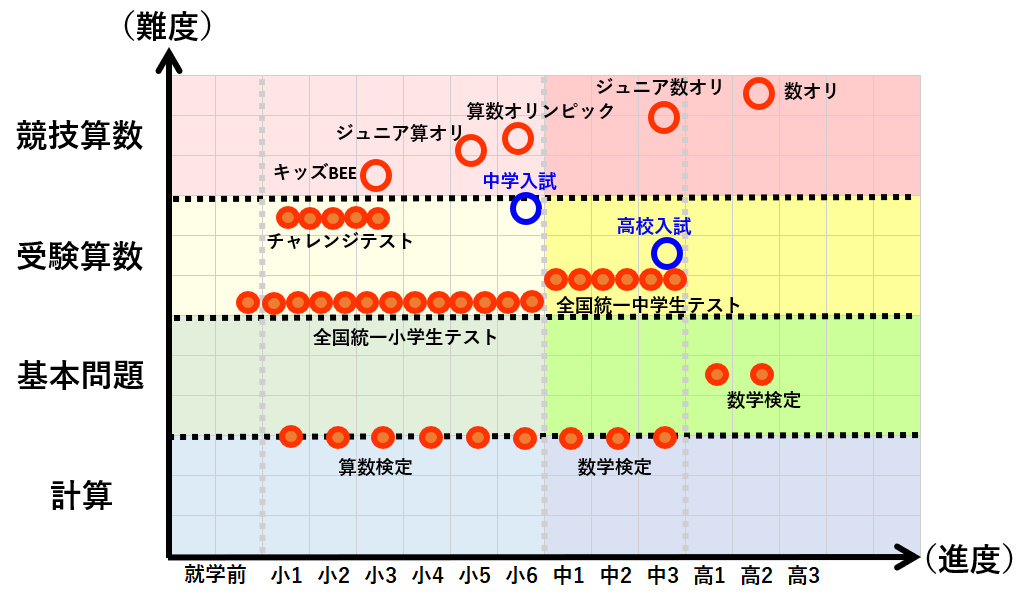
この算数・数学のフィールドは広大で、闇雲に進むのは非常に難しく思えます。そこで、このフィールド上に特定の試験等をプロットし、今の居場所から近い所を目標として学習を行っていきました。

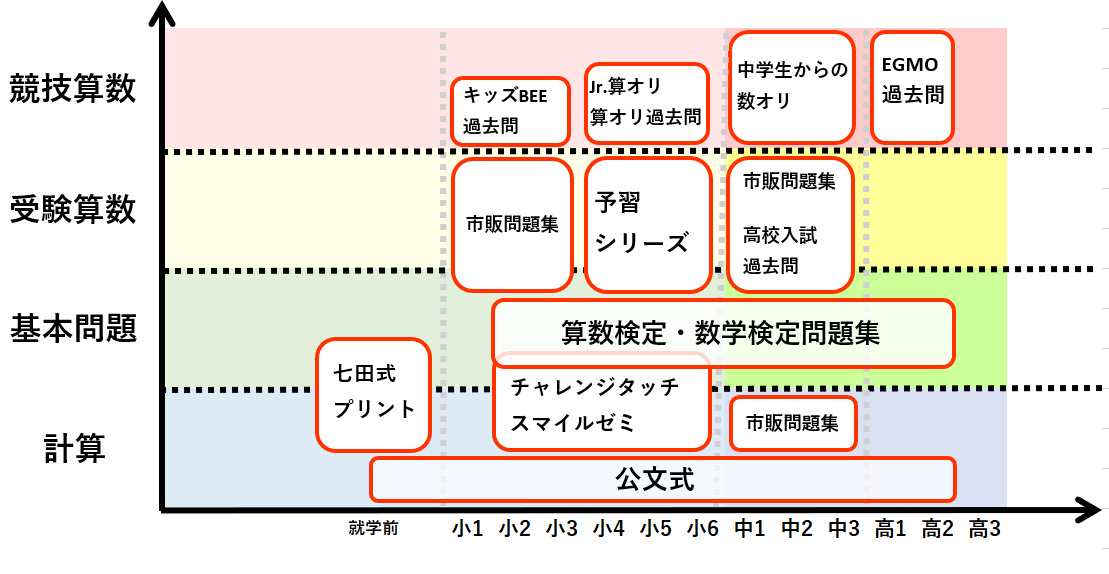
ちなみに使用した教材は、ざっくり示すと下図のようになります。

定期メンテナンス

一度覚えたものは、しばらく使わないと忘れます。そのため、定期的に使っていくことが重要になります。

そこで我が家では1つの単元ごとに、易しいものから難しいものまで一気にやらず、期間を空けながら順番にやっていく方法を採りました。

1回目では進度を意識し、2回目以降で難度を上げていきます。これによって、理解を深めるだけでなく、昔やった単元を忘れることも防ぎました。

一例として「二次関数」の単元では下記のような感じです。

公文式で中高範囲の二次関数を学ぶ（小1～小2）
数学検定の対策（小2～小3）
高校入試数学（小5～小6）

ポイント取り組むタイミングや順番については、子供の興味を優先しました。
例えば小6までの算数を終えている状態で、次に中1の単元と小学校範囲の難問のどちらをやるのが良いのでしょうか。我が家では、子供が数検5級を取りたいなら中1の基本問題を網羅しますし、キッズBEEで入賞を目指したいなら小3の難問に取り組み、積分を知りたいなら中高範囲の計算問題のみを進めて高2範囲の積分まで最短ルートで行く、という感じです。どうせ最終的には全部やるので、順番はどうでも良い（従って子供がやりたいものをやりたい時にやった方が良い）というわけです。

他分野とのつながり

算数・数学は、他の科目や他の物事とも密接に繋がります。

例えば割合と比は日常的にも使いますし、理科の計算や社会の統計を読むのにも必要です。公文式ではやらないので、算数検定を前倒しして学びました。

また、子供が早い段階で物理や化学に興味を示したので、説明に必要となる三角関数や指数対数などは早めに教えました。

漠然と数学を進めるより、これが何の役に立つかを分かっている方が学ぶ意欲が上がるようです。また本人が必要と認識しているものは、一度習得した後も比較的忘れにくかったようにも思います。

コンテンツ一覧

- スポンサーリンク -