算数4年(上)第9回「いろいろな四角形」基本問題
予習シリーズ算数4年上・第9回「いろいろな四角形」
基本問題（予習シリーズP88～P89）の解説です！
基本問題1⃣（１）
四角形のまわりの長さというのは、四つの辺の合計です。
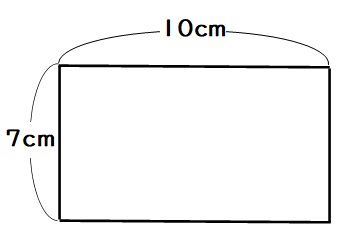
$$まわりの長さ＝7+10+7+10＝34$$
面積はたて×よこなので、
$$面積＝7×10＝70$$
答え：まわりの長さ＝34cm、面積＝70cm2
基本問題1⃣（２）
この問題のようにL字型のへこんだ形のまわりの長さを出すときは、ふくらませて長方形に直しましょう。
下の図で、青い線の長さと赤い線の長さは同じです。
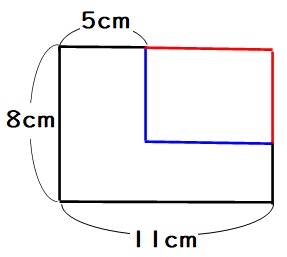
なので、下の2つの図形のまわりの長さは同じになります。
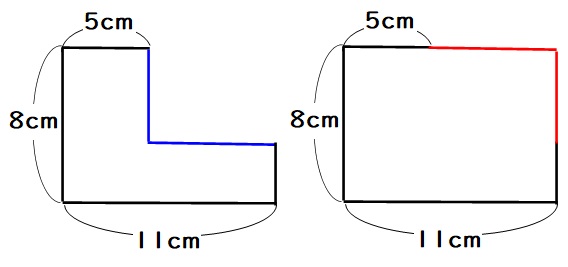
よってもとめる長さは、
$$8+11+8+11＝38$$
面積は、（Ａ）正方形を切り取る方法と（Ｂ）四角形2つに分ける方法があります。どちらでやってもOKです。
（Ａの場合）切り取った正方形の一片の長さは
$$11－5＝6$$
より、6cmであることが分かります。
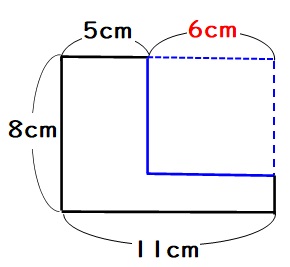
よってこの図形の面積は、たて8cm・よこ11cmの長方形からたて6cm・よこ6cmの正方形を引いて、
$$8×11－6×6＝52$$
答え：長さ＝38cm、面積52cm2
基本問題1⃣（３）
【ア】平行四辺形の向かい合う角度は等しいので、
ア＝61度となります。
まず下の図の赤い2つの直線は平行なので、錯角の関係から下図の赤い角度が61度と分かります。
次に、下の図の青い2つの直線が平行なので、同位角の関係から下図の青い角度も赤い角度と同じ61度と分かります。
【イ】下図の2つの赤い角度は同側内角なので、合計180度です。
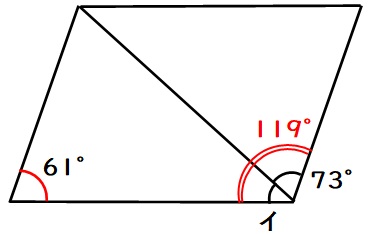
よって、右の二重線の角度は
$$180－61＝119$$
イの角度は
$$119－73＝46$$
イ＝46度
【ウ・エ】ひし形を対角線で分けると、4つの三角形は同じ形になります。
よってウ＝64度、エ＝58度です。
基本問題1⃣（４）
ア：平行四辺形の面積＝底辺×高さなので、
$$13×9＝117$$
答え：117cm2
イ：台形の面積＝（上底＋下底）×高さ÷2なので、
$$（5＋11）×9÷2＝72$$
答え：72cm2
ウ：ひし形の面積＝対角線×対角線÷2なので、
$$14×8÷2＝56$$
答え：56cm2
基本問題2⃣
台形の面積＝（上底＋下底）×高さ÷2なので、
$$(6＋下底)×8÷2＝68$$
$$(6＋下底)×8＝68×2＝136$$
$$(6＋下底)＝136÷8＝17$$
$$6＋下底＝17より、下底＝11$$
答え：11cm
基本問題3⃣
四角形の性質は覚えておくことが望ましいですが、覚えていない場合はその場で四角形を書いて自分で確認してみましょう。
| 辺の平行 | 辺の長さ | 角度 | |
|---|---|---|---|
| 正方形 | 2組 | 4辺が等しい | 直角4つ |
| 長方形 | 2組 | 2辺等しい | 直角4つ |
| ひし形 | 2組 | 4辺が等しい | 向かい合う角が同じ |
| 平行四辺形 | 2組 | 2辺等しい | 向かい合う角が同じ |
| 台形 | 1組 |
| 対角線同士の角度 | 対角線の長さ | 真ん中で交わる | |
|---|---|---|---|
| 正方形 | 直角 | 同じ | ○ |
| 長方形 | － | 同じ | ○ |
| ひし形 | 直角 | － | ○ |
| 平行四辺形 | － | － | ○ |
| 台形 | － | － | × |
（１）対角線が直交するのは正方形とひし形
答え：アとエ
（２）となりあう角度が等しいのは正方形と長方形（90度で等しい）
答え：アとイ
（３）1組の辺が平行で長さが等しいのは正方形、長方形、平行四辺形、ひし形
答え：アとイとウとエ
（４）向かい合う2組の辺の長さが等しいのは正方形、長方形、平行四辺形、ひし形
答え：アとイとウとエ
基本問題4⃣
（１）平行四辺形の面積＝底辺×高さなので、
$$30×20＝600$$
答え：600cm2
（２）平行四辺形を横に倒すと下図のようになります。
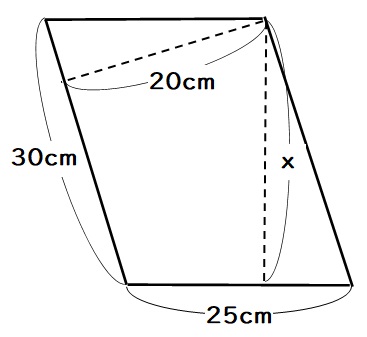
平行四辺形の面積＝底辺×高さの式をこの向きで使うと、
$$25× ｘ ＝600$$
$$ｘ＝600÷25＝24$$
答え：24cm
コメント