算数4年(上)第9回:いろいろな四角形 応用問題解説
予習シリーズ算数4年上・第9回:いろいろな四角形
応用問題A・応用問題B(最難関問題集P36~P39)の解説です!
応用問題A1⃣
(1)錯角の関係から、下図の赤い角度は70度です。
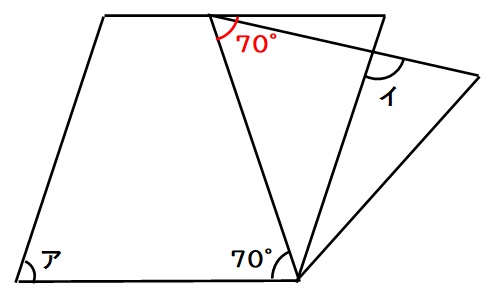
次に、下図の青色三角形ECDを見ると、ECとDCが同じ長さなので、三角形ECDは二等辺三角形です。よって青い角度は70度です。
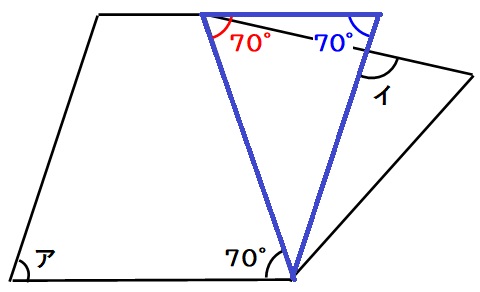
最後に、四角形ABCDはひし形なので、向かい合う角度は同じです。
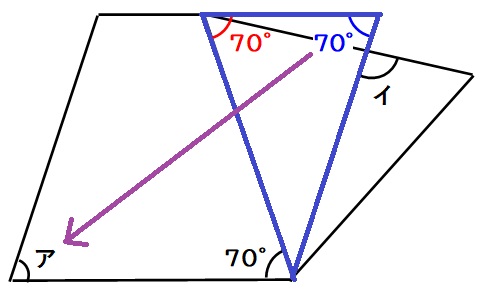
答え:70度
【別解】下図の2本の赤い線は長さが同じで、上底と下底が平行なので、四角形ABCEは等脚台形(左右対称、真ん中で折ると重なる)です。
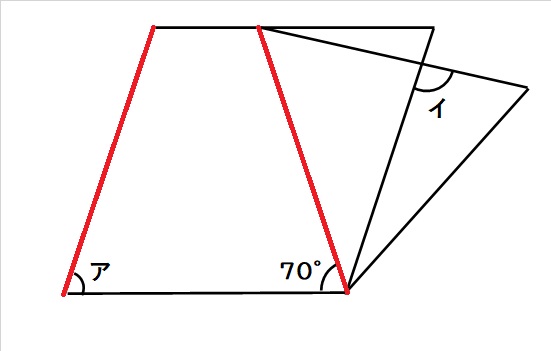
よってアは70度です。
(2)三角形CEF(下図の紫色)は正三角形なので、角度は60度です。
よって、下図の緑色の角度は70-60=10度となります。
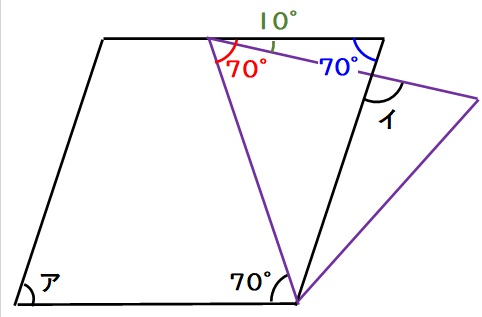
よって、イの対頂角の角度は
180-10-70=100度
対頂角の関係から、イも100度となります。
答え:100度
応用問題A2⃣
(1)長方形全体の面積は
$$24×42=1008$$
アとイの面積は等しいので、アの面積は
$$1008÷2=504$$
答え:504cm2
(2)アのまわりの長さとイのまわりの長さを見比べると、下図の赤線と緑線は長さが共通です。
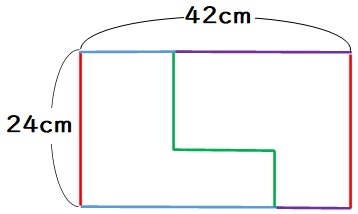
なので、アのまわりの長さがイより10㎝長いというのは、上図の青色の合計が紫色の合計より10cm長いということになります。
青色と紫色の合計の長さは、42cmが2本ですから84cmです。
つまり青色と紫色は和が84cmで差が10cmなので、和差算を使って
$$青色=(84+10)÷2=47cm$$
青色の2本の線は、よく見ると差が15cmになっています。そのため、上の青線の長さは
$$(47-15)÷2=16$$
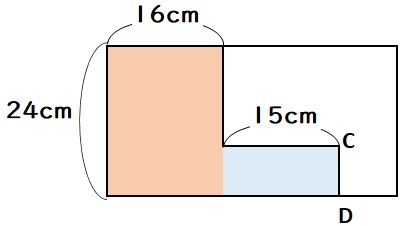
上図の赤い面積は24×16=384cm2なので、青い面積はアから384を引いて
$$504-384=120$$
よってCDの長さは
$$120÷15=8$$
答え:8cm
応用問題A3⃣
(1)折れ線の短い1本ずつの長さはどれも2cmなので、
$$2×8=16$$
答え:16cm
(2)アの部分には2×2の正方形が15個あることが分かります。
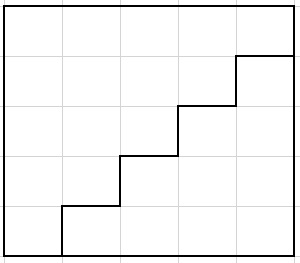
よって面積は
$$2×2×15=60$$
答え:60cm2
応用問題A4⃣
(1)アは平行四辺形なので、面積は
4×3=12cm2
アとイの面積は同じなので、台形イの面積も12cm2
答え:12cm2
(2)ウはアより9cm2大きいので、アとイとウの面積の合計は
$$12+12+(12+9)=45$$
大きな台形ABCDの面積が45cm2なので、台形の面積の公式に当てはめて、
$$(4+下底)×5÷2=45$$
$$(4+下底)×5=90$$
$$(4+下底)=18$$
下底=14
答え:14cm
応用問題B1⃣
まず重なっていて見えない部分を図に書いてみます。
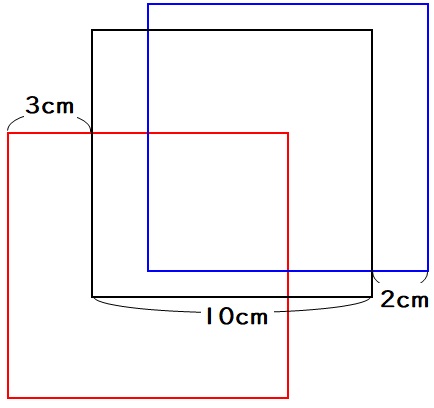
この図形の横の長さは、上図の長さを参考に
3+10+2=15cm
もしも赤い正方形と青い正方形が全く重なっていないとしたら、この図形全体の横の長さは20cmになるはず。
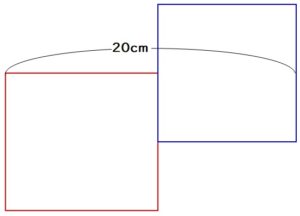
しかし横の長さは15cmしかないので、
$$20-15=5$$
赤い正方形と青い正方形は5cm重なっていることが分かります。
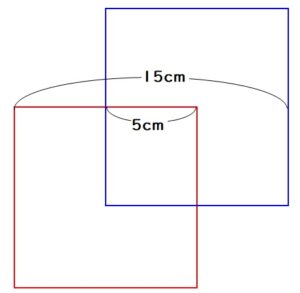
次にこの図形のまわりの長さを考えます。まわりの長さは下図の大きな緑色の四角形と同じになるので、
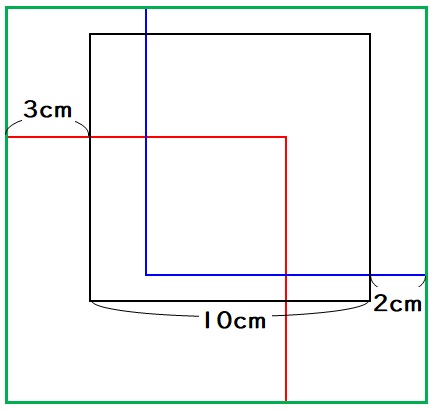
$$15+15+たて+たて+=60cm$$
よって、たての長さは15cmです。
ここで先ほどと同様に、もしも赤い正方形と青い正方形が重なっていないとしたらたての長さは20cmであるはずなので、赤い正方形と青い正方形はたて方向にも5cm重なっていることが分かります。
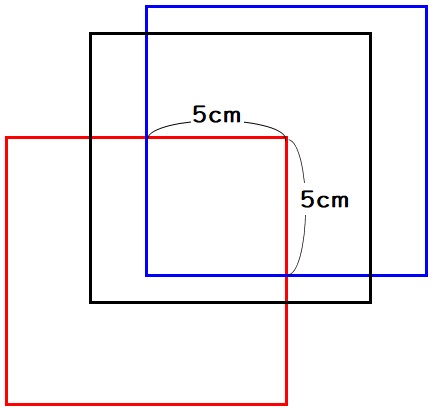
よって、赤い正方形と青い正方形の重なっている部分は5cm×5cmであることが分かります。
$$5×5=25$$
答え:25cm2
応用問題B2⃣
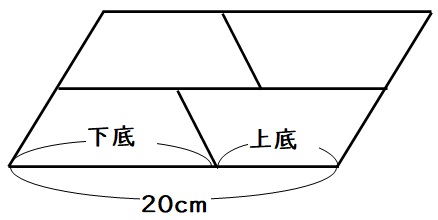
(1)図1を見ると、台形の上底+下底=20cmだと分かります。
いっぽう図2のまわりの長さは、上底4つと下底4つの合計です。
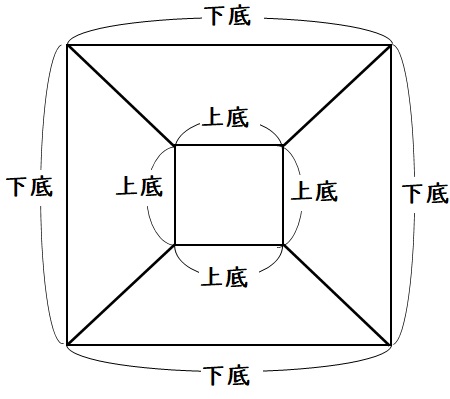
よって、まわりの長さは
$$20×4=80$$
答え:80cm
(2)図1の大きな平行四辺形の面積を考えると、
$$20×高さ÷160$$
図1の高さは8と分かります。よって、台形1個の高さはその半分で4cmです。
図2に注目すると、下図のように

$$4+下底+4=上底$$
であることが分かるので、
$$上底-下底=8$$
これと、一番最初に調べた「上底+下底=20」を和差算して、
$$上底=(20+8)÷2=14cm$$
$$下底=20-14=6cm$$
となります。
図2の内側の正方形は1辺の長さが台形の下底と同じなので、面積は
$$6×6=36$$
答え:36cm2

コメント