算数4年(上)第5回「総合」 応用問題解説
予習シリーズ算数4年上・第5回「総合」
最難関問題集P20~P23の解説です!
応用問題A1⃣
【出題範囲:第1回】
(1)
\begin{cases}
20題×23日(1日目~23日目)\\
5題×1日(24日目)\\
\end{cases}
問題集の問題数は、
$$20×23+5=465$$
問題は1ページに15題のっているので、
$$465÷15=31$$
答え:31ページ
(2)
14日目までに解いた問題数は
$$20×14=280$$
よって、15日目の最初の問題は281題目です。
281題目がのっているページは、
$$281÷15=18あまり11$$
よって、19ページ目の11題目が281題目です。
答え:19ページ目の11題目
応用問題A2⃣
【出題範囲:第2回】
(1)3×イの下1ケタが7であることに注目します。
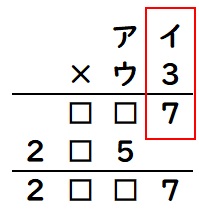
イ=9と決まります。
次に、ウ×9の下1ケタが5なことに注目します。
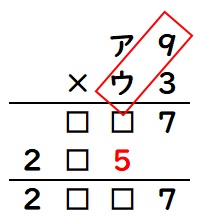
ウ=5と決まります。
ア9×5の百の位が2なので、アは4か5と分かります。
しかし、もしもアが5だとすると、実際に計算をしてみると、最後の答えの千の位は2ではなく3となってしまいます。
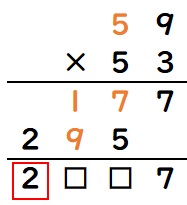
そのため、アは4しか入りません。
答え:ア=4、イ=9、ウ=5
(2)まず、割られる数の下1ケタの4を下におろしてみると、
カ×9の下1ケタが3であることが分かります。
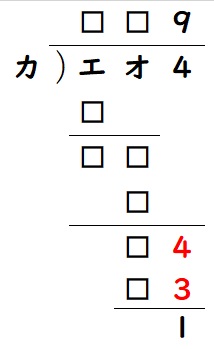
よって、カは7に決まります。
次に、100の位と10の位の計算で、カ×□の答えが1ケタになっていることに注目。
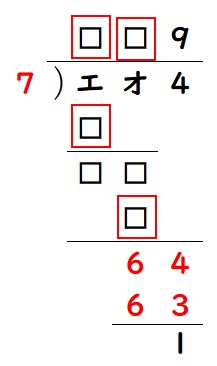
□は1と分かります。
最後に、分かる部分を順番に埋めて行くと、
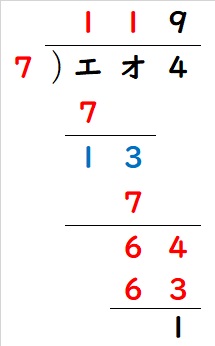
エ=8、オ=3となります。
答え:エ=8、オ=3、カ=7
応用問題A3⃣
【出題範囲:第4回】
A<B<Cなので、
A+B、A+C、B+Cの大きさを比べると、
A+B<A+C<B+Cとなります。
よって、
\begin{cases}
A+B=43\\
A+C=70\\
B+C=81\\
\end{cases}
ここで「A+C」と「B+C」の差について考えてみます。
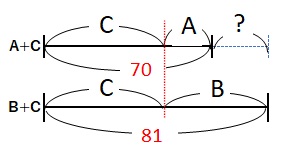
AとBの差は上の線分図の「?」の部分となります。
$$81-70=11$$
AとBの差は11となります。
答え:11
(2)
\begin{cases}
A+B=43\\
B-A=11\\
\end{cases}
AとBの和差算を解いて、
\begin{cases}
A=(43-11)÷2=16\\
B=16+11=27\\
C=81ー27=54\\
\end{cases}
答え:A=16、B=27、C=54
応用問題A4⃣
【出題範囲:第3回・第4回】
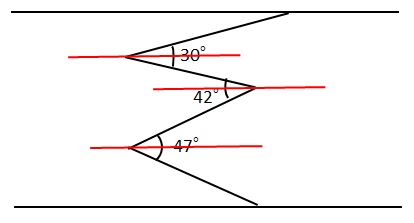
★2つの合計は42°です。
アとイに錯角を使うと、
30°=ア+★
42°=イ+★
なので、
ア+★+イ+★=30+47=77°となります。
★2つの合計は42°だったので、
ア+イ=77ー42=35°
問題文より、アはイより7度小さいので、和差算を使って、
ア=(35ー7)÷2=14°
イ=14+7=21°
答え:ア=14°、イ=21°
【別解】四角形の内角の和が360°であることを使います。
下図の赤線のように延長線を引き、角度を求めます。
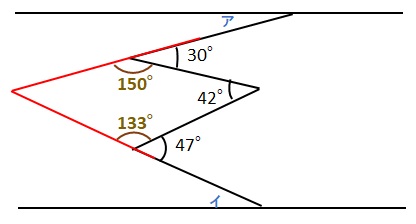
四角形の内角の和は360°なので、四角の左の角度は
360ー150ー42ー133=35°となります。
ここに直線あ・いに平行な補助線を引くと、
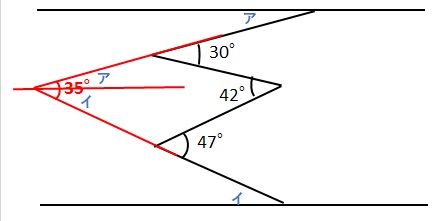
ア+イ=35°であることが分かります。
問題文より、アはイより7度小さいので、和差算を使って、
ア=(35ー7)÷2=14°
イ=14+7=21°
答え:ア=14°、イ=21°
応用問題A5⃣
【出題範囲:第2回】
(1)9×5+(5+3)=53
答え:53
(2)一の位×5+(十の位+3)=23となるので、
一の位×5+十の位=20
これを満たす一の位と十の位の組み合わせを考えると
\begin{cases}
一の位が4で十の位が0 ×\\
一の位が3で十の位が5 ○\\
一の位が2で十の位が10 ×\\
一の位が1で十の位が15 ×\\
一の位が0で十の位が20 ×\\
\end{cases}
十の位が10以上になるのはおかしいですし、十の位が0になるのもおかしいです。
一の位が3で十の位が5の時のみ成立するので、答えは53となります。
答え:53
応用問題A6⃣
【出題範囲:第1回】
(1)あつし君とけんじ君を比べるとこのようになります。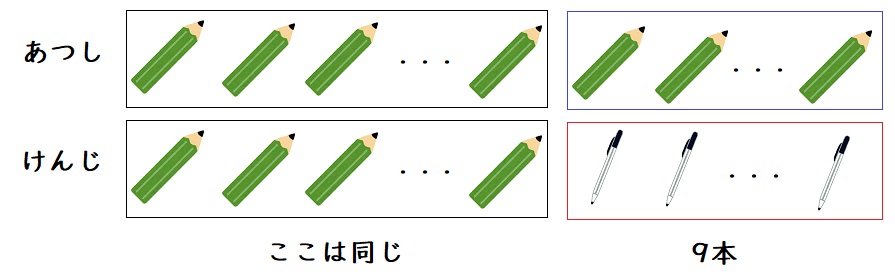
あつし君とけんじ君の違いは、えんぴつ9本とボールペン9本の違いなので、
$$(80ー45)×9=315$$
答え:315円
(2)さとし君はけんじ君よりも290円多く払ったので、
さとし君とあつし君を比べると、
$$290+315=605$$
さとし君はあつし君よりも605円多く払ったことが分かります。
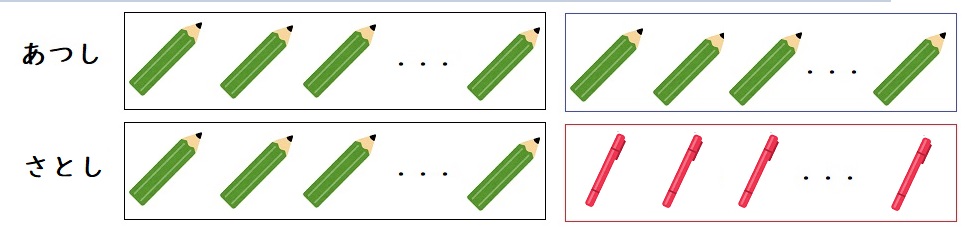
えんぴつとサインペンの値段の違いは
$$100ー45=55円$$
なので、さとし君が買ったサインペンの本数は
$$605÷55=11本$$
さとし君はえんぴつとサインペンを同じ本数買ったので、さとし君が買った本数の合計は
$$11×2=22本$$
けんじ君もさとし君と同じ本数を買ったので、22本となります。
けんじ君が買ったボールペンは9本だったので、
けんじ君が買ったえんぴつは
$$22ー9=13本$$
答え:13本
応用問題A7⃣
【出題範囲:第3回】
折った紙を全部開いた図を考えてみます。

上の図で2つの●は折った場所なので角度は同じです。
また、赤線のように錯覚を使って、●=75°です。
次に、2つ目の折り線だけを開いた図を考えます。
下図のように、同位角で150°を移せます。
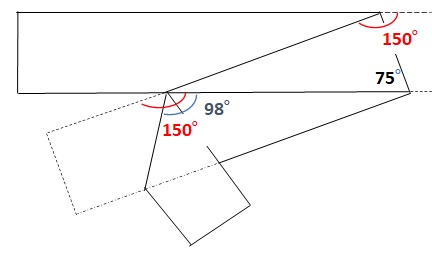
上図の150°と98°の差を考えると、
$$150ー98=52°$$
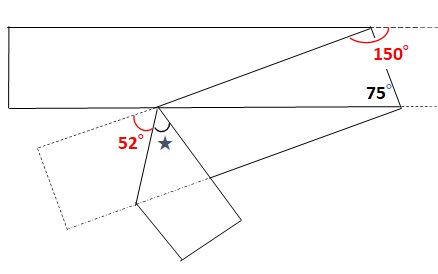
折り目を考えると、上図の★は52°と同じです。
最後に、下図の104°を同位角でアに移して、アも104°となります。
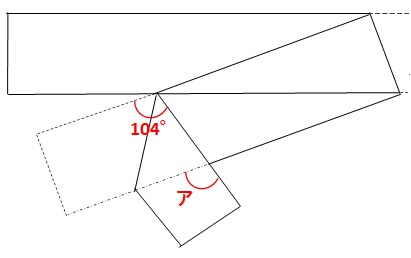
答え:104°
応用問題A8⃣
【出題範囲:第4回】
(1)父、母、兄、弟の平均は28歳なので、合計は
$$28×4=112$$
父+母は兄+弟より64歳多いので、下図のようになります。
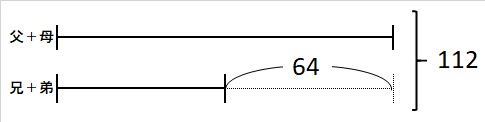
父+母の年令は
$$(112+64)÷2=88$$
答え:88才
(2)父+兄は母+弟より10歳多いので、下図のようになります。
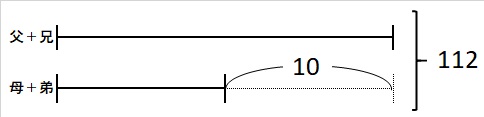
父+兄の年令の合計は
(112+10)÷61
父+兄が61才で、父+母が88才なので、母と兄の差は
88ー61=27
答え:27才
(3)母と兄の差が27歳で、花子さんは兄より3才年下なので、
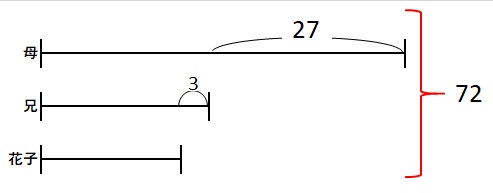
兄の年令は(72ー27+3)÷3=16才
(1)で使った線分図を使うと、

兄+弟=(112ー64)÷2=24才
よって弟の年令は
24ー16=8
答え:8才

コメント