算数4年(上)第8回 応用問題解説（最難関問題集）

算数4年(上)第8回：三角形の角 応用問題解説

予習シリーズ算数4年上・第8回：三角形の角

応用問題A・応用問題B（最難関問題集P32～P35）の解説です！

応用問題A1⃣

下図の2本の赤い線は長さが同じです。

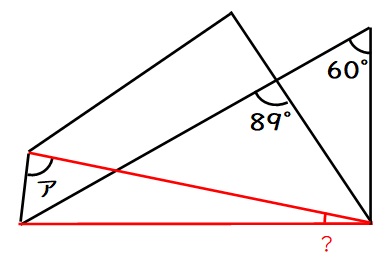
そのため、上図の「？」の角度が分かれば、二等辺三角形の性質でアの角度が求まることが分かります。

下図のように、青い三角形の外角定理で青い角度は29度と分かります。

また、三角定規なので緑の角度は45度です。

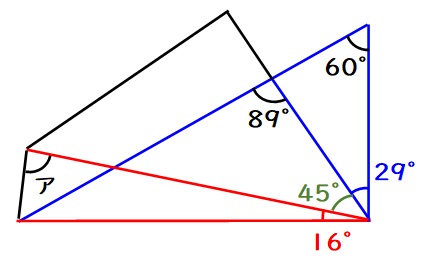
よって赤い？の角度は

$$90－29－45＝16度$$

したがって、アの角度は

$$(180－16)÷2＝82度$$

答え：82度

応用問題A2⃣

（１）まずDC＝DEより、下図の赤い線の長さが同じなので、二等辺三角形の性質を利用して、

∠E＝64度となり、残りの角度が

$$180－64－64＝52度$$

となります。

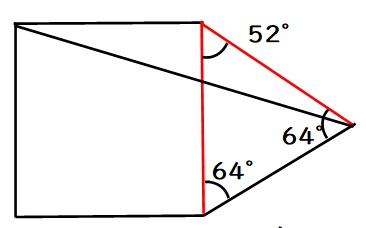
また、四角形が正方形なので、下の2つの青線の長さも同じです。

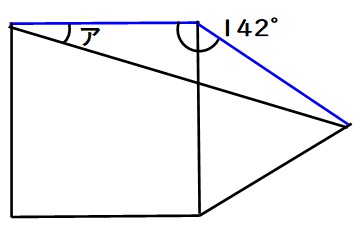
二等辺三角形の性質より、142度以外の残りの2つの角度は同じなので、

$$(180－142)÷2＝19度$$

答え：19度

（２）正方形の角度は対角線でちょうど半分になるので、

下図の赤い角度は45度となります。

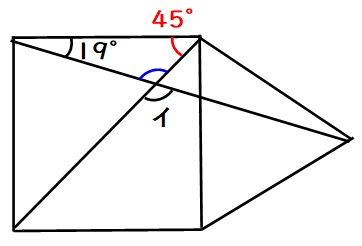
上図の青い角度は、

$$180－19－45＝116度$$

この青い角度はイの対頂角なので、イも116度となります。

答え：116度

応用問題A3⃣

（１）四角形の内角の和は360度なので、下図の赤い角度は

$$360－35－65－33＝227度$$

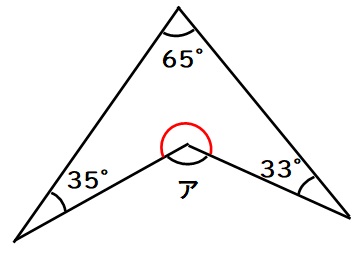
赤い角度とアを合わせるとちょうど1周(360度)なので、アの角度は

$$360－227＝133度$$

答え：133度

（２）下図の赤い角度は、外角定理より

$$17＋28＝45度$$

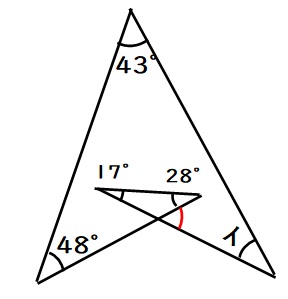
よって、下図の青い角度は、

$$180＋45＝225度$$

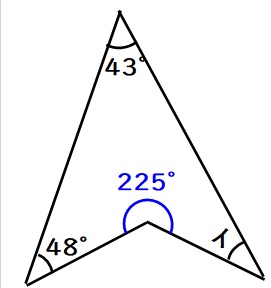
四角形の内角の和は360度なので、角イは

$$360－48－43－225＝44度$$

答え：44度

応用問題A4⃣

下図のように、二等辺三角形で角度が同じ部分に印をつけます（●と◆）。

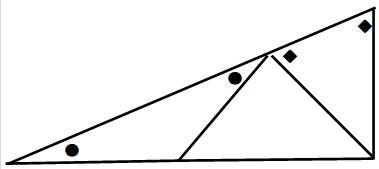
一番大きな三角形に注目すると、●＋◆＋90度＝180度なので、

●＋◆＝90度であることが分かります。

次に、下図の赤い三角形に注目します。

赤い角度は、180度から●と◆を引いたものですが、

先ほど●＋◆＝90度と分かったので、赤い角度は

$$180－90＝90度$$

となります。また、赤い三角形は二等辺三角形です。そのため、残りの角度は45度と分かります。

アの角度は、直角から45度を引いて

$$90－45＝45度$$

答え：45度

【別解】

最初に、左端の角度を①とします。

ADとDEの長さが等しいので、二等辺三角形の性質を使って下のようになります。

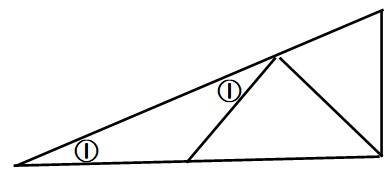
赤い部分に注目すると、外角定理が使えます。外角部分の角の大きさは②です。

二等辺三角形の性質から、その右の角度も②です。

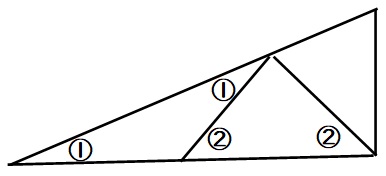
下図の赤線で外角定理を使い、外角部分の角の大きさは3となります。

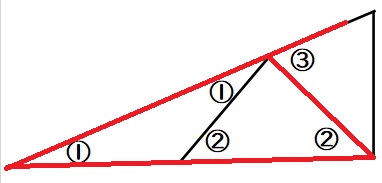
二等辺三角形の性質から、もう1つの角度も③です。

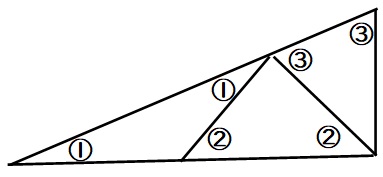
ここで一番大きな直角三角形(下図の青線)に注目。

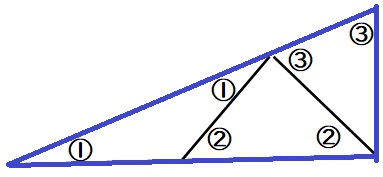
①＋③＝90度なので、①の大きさは

$$90÷4＝\frac{90}{4}＝\frac{45}{2}度$$

③の大きさはこの3倍なので、

$$\frac{45}{2}×3＝\frac{135}{2}$$

三角形の内角の和から、③＋③＋ア＝180度なので、

$$ア＝180－\frac{135}{2}×2＝45度$$

答え：45度

応用問題B1⃣

下図の赤い三角形に注目します。

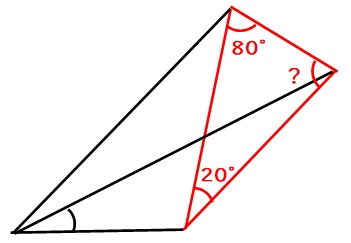
残った？の角度を求めると、

$$180－20－80＝80度$$

なので、この赤い三角形は80度、80度、20度の二等辺三角形です。

次に、下図の青い三角形に注目します。

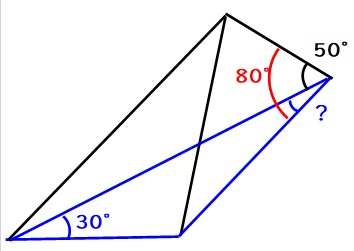
この三角形の青い？の角度は、

$$80－50＝30度$$

ですから、青い三角形は30度を2つ持っている二等辺三角形です。残りの角度は

$$180－30－30＝120度$$

です。

ここまでの話をまとめると、下図の赤い三角形と青い三角形はどちらも二等辺三角形だということが分かりました。

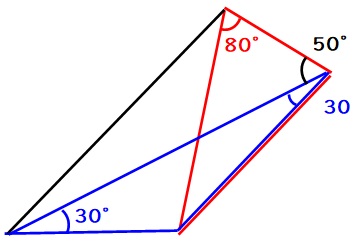
なので、下図の2つの緑色の辺の長さは同じです。

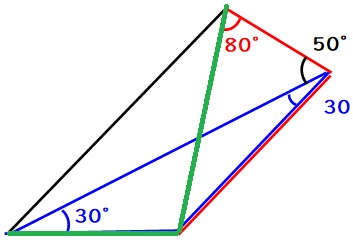
つまり、下図の緑色の三角形も、二等辺三角形です。

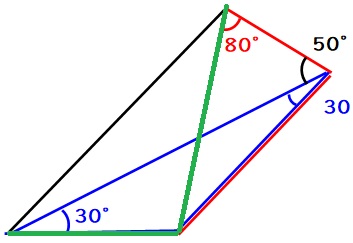
この緑色の三角形の一番大きい角は、

$$120－20＝100度$$

です。よって残りの角度の大きさは

$$(180－100)÷2＝40度$$

となります。

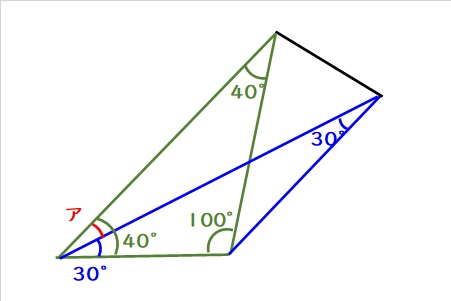
よって、アは

$$40－30＝10度$$

答え：10度

応用問題B2⃣

下図で、赤い線と青い線はそれぞれ同じ長さです。

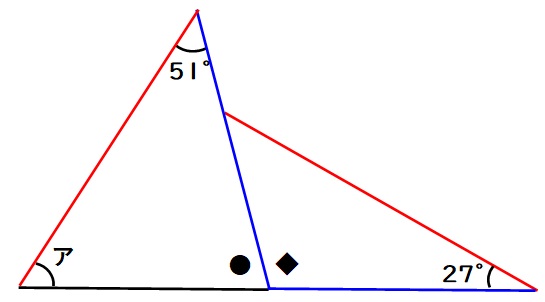
右の三角形をくるっとひっくり返して下図のようにすると、大きな三角形ができます。

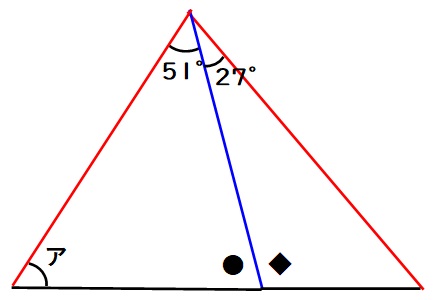
大きな三角形は、赤い線の長さが同じなので、二等辺三角形であることが分かります。

上の角度が分かっているので、残りの2つの角度は

(180－51－27)÷2＝51度

よって、アは51度です。

答え：51度

【参考：上の図が大きな三角形になっていることの確認】

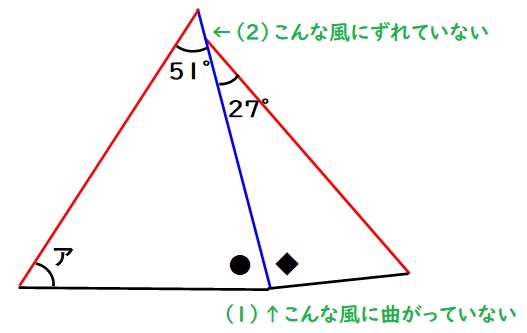
（１）最初の図で、●と◆は合わせて180度です。そのため、右の三角形をくるっとひっくり返しても、●と◆は合わせて180度なので、この三角形の底辺は直線になります。

（２）また、青い線は同じ長さなので、三角形の上の頂点の部分は1点で交わっています。

よって、大きな三角形が1つ作れたと言えます。