算数4年(上)第2回:計算のきまり 基本問題
予習シリーズ算数4年上・第2回:計算のきまり
基本問題(予習シリーズP22~P23)の解説です!
基本問題1⃣
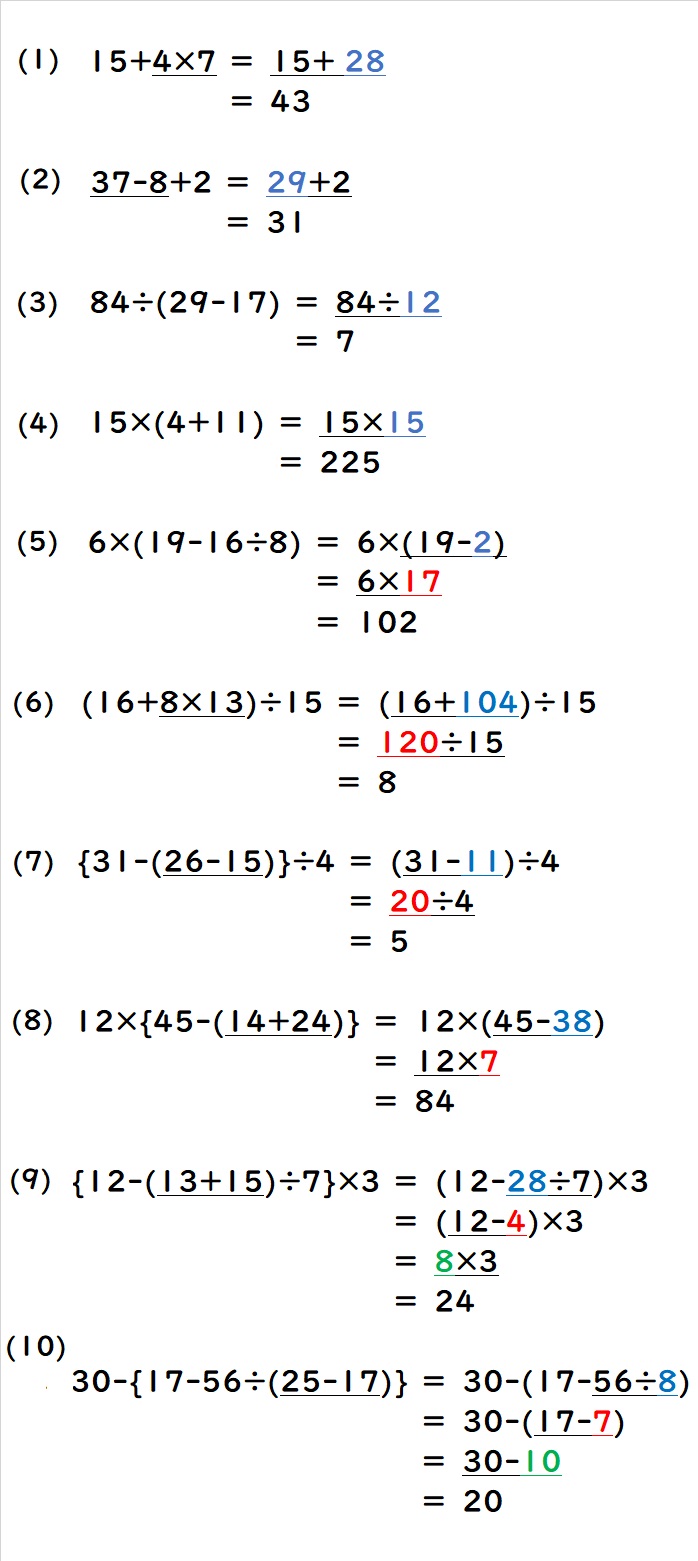
基本問題2⃣
逆算は「たし算とひき算」「かけ算とわり算」でそれぞれセットになります。ただしひき算の逆算が必ずたし算とは限りません。7-□=2の□は引き算で出します。
(1)□に12を足して25だから、□は25より12小さい。
$$□=27-12=15$$
(2)□から19を引いて15だから、□は15より19大きい。
$$□=15+19=34$$
(3)□が7個で56だから、
$$□=56÷7=8$$
(4)□を6人で分けると1人12個だから、
$$□=12×6=72$$
(5)23に□を足すと41だから、□は41より小さい。
$$□=41-23=18$$
(6)38から□を引くと25だから、□は38より小さい。
$$□=38-25=13$$
(7)6が□個で78だから、□は78より小さい。
$$□=78÷6=13$$
(8)72を□人で分けると1人18個だから、□は72より小さい。
$$□=72÷18=4$$
(9)「3×□」がいくつか分かれば解けるので、「3×□」を1つの大きな□と考えてしまうと分かりやすいです。
$$3×□=16+5=21\\
□=21÷3=7$$
(10)「13-□」がいくつか分かれば解けるので、「13-□」を1つの大きな□と考えてしまうと分かりやすいです。
$$13-□=28÷4=7\\
□=13-7=6$$
基本問題3⃣
文章題を式に直す練習です。「ある数」が分からないので、「ある数」を□として式を作ってみましょう。慣れないうちは、文章を一気に全部読んで一気に式を作ろうとせず、少しずつ読んで少しずつ式にしていきましょう。
「ある数と3の和」
$$□+3$$
「ある数と3の和の2倍」
$$(□+3)×2$$
「25からある数と3の和の2倍をひいた」
$$25-(□+3)×2$$
「25からある数と3の和の2倍をひいたところ、答えが9になりました」
$$25-(□+3)×2=9$$
後はこの式を解くだけです。
$$25-(□+3)×2=9\\
(□+3)×2=16 ←25-9で計算\\
□+3=8 ←16÷2=8で計算\\
□=5$$
基本問題4⃣
くふうして計算する問題は、くふうしなくても気合で解けてしまいます。しかしそれだと、今後予習シリーズを進めていくうちに後で困ることになります。なんでもいいから答えを出すのではなく、くふうをする練習をしましょう。
今回特に覚えたいくふうは3つです。
- 25×4=100になって次の計算がしやすくなる
※125×8=1000もありますが、今回は出てこないです。
- 結合法則で集めて10や100などキリが良い数字にする
※例えば「6×88+6×12」は、6が88個と6が12個の合計ですから、6が100個の合計と同じことになります。「6×114-6×14」は、6が114個ある所から6を14個引くので、6が100個と同じになります。
- キリのよい数字に近い数字を、分配法則で100と残りに分けて計算しやすくする
※例えば98は100に近いので、100-2に分けてしまいます。98×31は計算しにくいですが、(100-2)×31とすれば3100-62なので暗算が可能になります
(1)
$$19×4×25\\
=19×100\\
=1900$$
(2)
$$99×7\\=(100-1)×77\\=7700-77\\=7623$$
(3)
$$73×41+27×41\\=(73+27)×41\\=100×41\\=100$$
(4)
$$49×112-12×49\\=49×(112-12)\\=49×100\\=4900$$
基本問題5⃣
□のあるひっ算では、くり上がり・くり下がりに気を付けましょう。
(1)貸し借りのない右の位から順番にやるのが良いでしょう。
まず一の位を考えます。
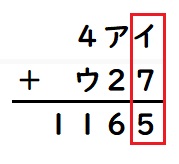
イ+7の答えが5にはならないので、イ+7=15とわかり、イ=8です。
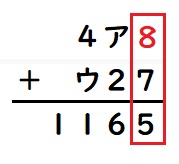
次に十の位を考えます。
1の位の答えが15なので、十の位の答えに1くり上がってきます。
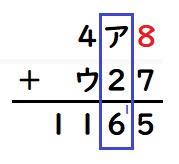
なのでア+2+1=6 となります (+1はくり上がりの分)
よって、ア=3となります。
最後に百の位ですが、今度は十の位でくり上がりが起きていないので、
4+ウ=11です。
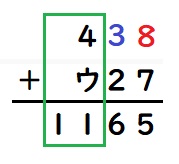
ウ=7となります。
答え:ア=3、イ=8、ウ=7
(2)今回も一の位からやっていきます。
一の位は 5-オ=9 ですが、この計算はできないので、十の位から1借りていることが分かります。
15-オ=9 となるので、オ=6
次に十の位を見ます。十の位は一の位に1貸していますので、
エ-7-1=0 となるので、エ=8
最後に百の位は十の位に貸していないので、
6-1=カ カ=5
答え:エ=8、オ=6、カ=5
(3)キとクがかくれているので、できる計算が6×5しかありません。
しかし5×6=30なので、答えの十の位は4になっているのはおかしいです。
つまり、この4は、ク×6の計算のくり上がりであることが分かります。
ク×6の答えは十の位が4で、1の位は問題を見れば8であると分かります。
なのでク×6=48です。
クが8であることが分かりました。
最後にまだ使っていない数字、答えの千の位の「1」に注目します。
キにどんな数字を入れれば、答えの千の位が1になるでしょうか。
6×2=12か6×3=18が考えられますが、試しに3を入れてみると、下の位の計算のくり上がりによって千の位が2になって失敗します。なのでキは2となります。
キとクが分かったので、最後に確認のために全体の計算をします。
答え:キ=2、ク=8、ケ=5

コメント