算数4年(上)第2回 応用問題解説（最難関問題集）

算数4年(上)第2回：計算のきまり 応用問題解説

予習シリーズ算数4年上・第2回：計算のきまり

応用問題A・応用問題B（最難関問題集P8～P11）の解説です！

応用問題A1⃣

（１）

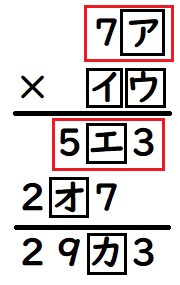
まず、７ア × ウ ＝５エ３となっている部分に注目します。

七十いくつかが五百いくつかになるためには、7倍か8倍をすることになります。（6倍では最大でも79×6＝474なので500にとどかないし、9倍では最小でも70×9＝630で600をこえてしまう）

しかし偶数・奇数のかけ算の関係に注目すると、アとウはどちらも奇数であることが分かります。

よって、ウは8ではなく7となります。ウ＝７

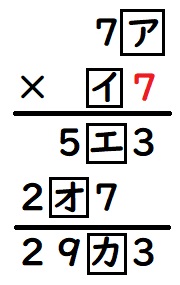
アは、7と掛けた答えの下1ケタが3ですから、ア＝９です。また、エ＝５です。

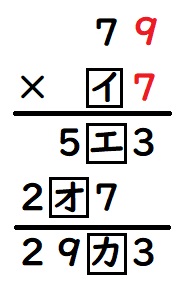
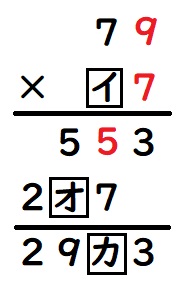
次に、下の足し算部分を計算します。オ＝３，カ＝２

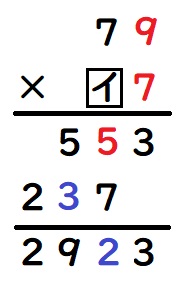
最後に、７９×イ＝２３７なので、イ＝３です。

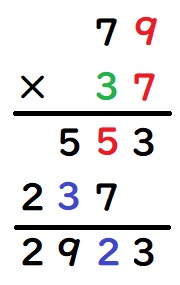
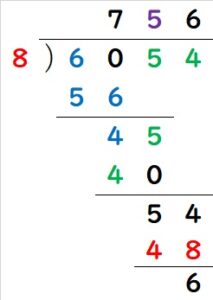
（２）

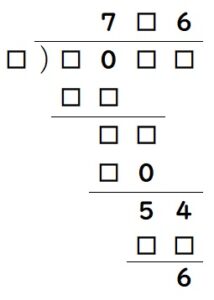
まず最初に一番下の□□が、５４－６＝４８となります。

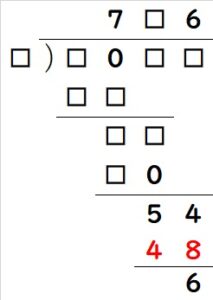
また、6を掛けて48になっているので、割る数は8です。

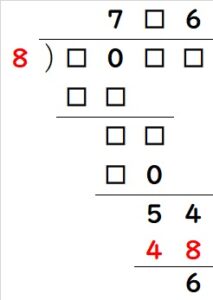
次に、１００の位の計算で、８×７＝５６が分かります。

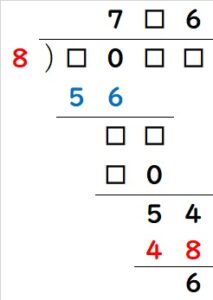
ひき算を考えると、その周辺も分かります。

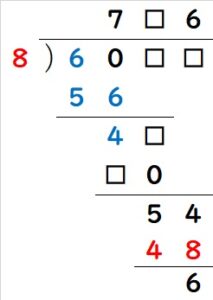
他にもわかる部分を全部うめて行きます。

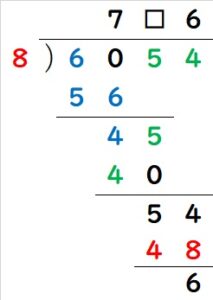
最後に残った□は、８×□＝４０より、□＝５となります。

応用問題A2⃣

\begin{cases}
A×C＝E\\
D÷C＝C\\
E－A＝B\\
\end{cases}

一番組み合わせが少ないのは2つ目の式です。D＝C×Cなので、以下の3通りしか組み合わせがありません。

• C＝1、D＝1
• C＝2、D＝4
• C＝3、D=9

C＝1、D＝1ではCとが同じになってしまうのでダメです。よって、可能性は2つにしぼられました。Cは2か3のどちらかです。

次に考えられる組み合わせが少ないのは、1番目の式「A×C＝E」です。

Cは2か3のどちらかであることを考えると、Eが10以上にならないような組み合わせは、以下の3通りしかありません。

• 4×2＝8（A＝4、C＝2、E＝8）
• 3×2＝6（A＝3、C＝2、E＝6）
• 2×3＝6（A＝2、C＝3、E＝6）

最後に残った3番目の式「Ｅ－Ａ＝Ｂ」に、上の条件を順番に当てはめてみます。

• ８－４＝４　…AもBも4になってしまうのでダメ
• ６－３＝３　…AもBも3になってしまうのでダメ
• ６－２＝４　…A＝2、B＝４　OK

答え：A＝2、B＝４、C＝3、D＝９、E＝6

応用問題A3⃣

（１）ある数を□とすると、

$$□＋３÷２＝７$$

ということですから、これを逆算して、

$$□＝７×２ー３＝１１$$

答え：11

（２）

$$Aの箱：13×3＋2＝41$$

$$Bの箱：41＋3÷2＝22$$

答え：22

（３）

$$Bの箱：□＋3÷2＝△$$

$$Aの箱：△×3＋2＝20$$

Aの箱から20が出てきたので、まずはAの箱を逆算します。

$$△＝(20－2)÷3＝6$$

Aに入れた数字は6です。これがBの箱から出てきたわけですから、Bの箱を逆算して、

$$□＋3÷2＝6$$

$$□＝6×2－3＝９$$

答え：９

応用問題A4⃣

（１）実際に計算できそうなので、計算してみましょう。

1回目：10は2で割り切れるので、10÷2＝5

2回目：5は2で割り切れないので、5＋1＝6

3回目：6は2で割り切れるので、6÷2＝3

ここで例に出てきている「3」が登場しました。ということは、この後は例と同じく、あと3回3→4→2→1となります。

4回目：3は2で割り切れないので、3＋1＝4

5回目：4は2で割り切れるので、4÷２＝２

6回目：6は2で割り切れるので、２÷2＝１

答え：6回

（２）

この問題の条件を簡単に言うと

1. 偶数なら÷2
2. 奇数なら+1

ということです。奇数を+1すると偶数になるので、2回連続で+1をすることはありません。

今回は5番目の結果が分かっているので、5番目から順番に見ていきます。

5回目の操作で1になったということは、5回目の操作は÷2です。もしも5回目の操作が+1だとすると、その前の数字が0だったことになってしまいます。÷2と+1を何度どのようにやっても0にはなりません。

ということは、4回目の操作で2になったことが分かります。

では4回目の操作は何だったかというと、4回目の操作は÷2です。+1だったらその前の数字が1だったことになります。しかし今回は5回目の操作で初めて1になったと書いてあるので、条件に合いません。

ということは、3回目の操作で4になったことが分かります。

1回目～3回目の操作は何だったかというと、+1の可能性も÷2の可能性もあります。

但し、2回連続で+1はしないことを考えると、

1. 「÷２」「÷２」「÷２」「÷２」「÷２」
2. 「＋１」「÷２」「÷２」「÷２」「÷２」
3. 「÷２」「＋１」「÷２」「÷２」「÷２」
4. 「÷２」「÷２」「＋１」「÷２」「÷２」
5. 「＋１」「÷２」「＋１」「÷２」「÷２」

以上の5通りが考えられます。

それぞれ逆算すると、順に32、15、14、12、5となります。

答え：32、15、14、12、5

応用問題B1⃣

十の位に最も小さい0と4を入れてみると、このようになります。

十の位の答えの方は4か5のどちらかですが、同じ数字は使えないので、５を入れます。

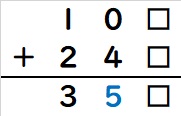
最後に残った数字（6、7、8、9）で、1の位にうまくあてはまるものを探します。

応用問題B2⃣

１は、4÷4＝１が使えそうです。

4をあと2個使わなければならないので、＋4－4などとして消してしまいましょう。

答え：４÷４＋４ー４＝１

２も、4÷4＝1が使えますね。1が2個集まれば2になってくれます。

答え：４÷４＋４÷４＝２

３は難問。一見4÷4＝1を使って4－1＝3の形が使えそうですが、4が1個余ってしまいます。

ここは、4を3つ集めて4で割ることで3を作りましょう。

答え：（４＋４＋４）÷４＝３

４のカードは最初から手元にあります。3枚の4をゼロにして消してしまえば答えになります。

答え：（４ー４）×４＋４＝４

5は難問。3の時と同様で、4を5個集めて4で割ることで5が作れます。

答え：（４×４＋４）÷４＝３

6も難問。３枚の４で何かをを作り、それと４を計算して６にする作戦でいきましょう。

• ３枚の４で２を作れば２＋４＝６
• ３枚の４で１０を作れば１０－４＝６
• ３枚の４で２４を作れば２４÷４＝６

（４＋４）÷４＝２で2が作れるので、これで６が作れました。

答え：（４＋４）÷4＋４＝６

７は簡単です。４＋４＝８と４÷4＝１が使えます。

答え：４＋４ー４÷4＝７

８も簡単。４＋４＝８なので、残った2個の4を消せばおしまいです。

答え：４＋４＋４ー4＝８

９も簡単。４＋４＝８と４÷4＝１が使えます。

答え：４＋４＋４÷4＝９