算数4年(上)第3回 応用問題解説（最難関問題集）

算数4年(上)第3回：角の性質 応用問題解説

予習シリーズ算数4年上・第3回：角の性質

応用問題A・応用問題B（最難関問題集P12～P15）の解説です！

応用問題A1⃣

見るからに対頂角が使えそうな問題です。

対頂角の関係から下図の2つの●の角度は同じで、その角度は180－125＝55°です。

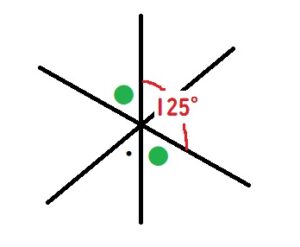
●と・の角度は等しいと書いてあるので、アは55+55=110°

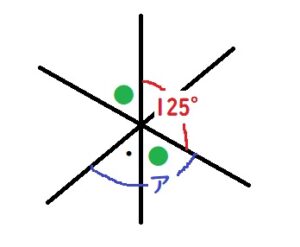
答え：110°

応用問題A2⃣

下図の赤線のように、直線あと直線いに平行な線（補助線）を引きます。

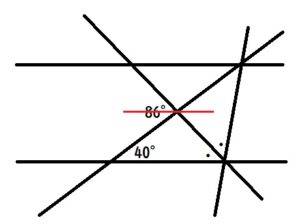
すると40°が錯角で移動できます。

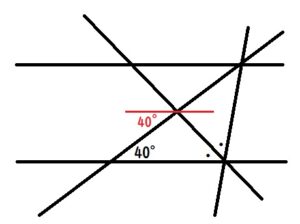
残った角度が86－40＝46°と分かり、46°も錯角で上に移動できます。

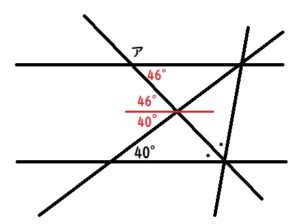
アは180ー46＝134°となります。

次にイを考えます。まずは86°のとなりの角度が

180－86＝94°であることが分かります。

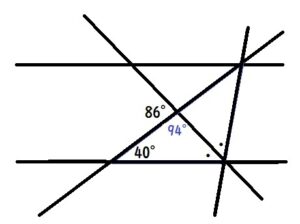
ウの角度は、下図の紫色の三角形の内角の和が180°であることより、

180－40－94＝46°となります。

ウとエの角度は同じなので、どちらも46°です。

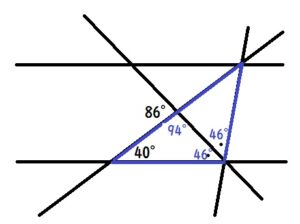
上の図の青い三角形の内角の和が180°なので、角イは

180ー40ー46ー46＝48°となります。

答え：ア＝134°、イ＝48°

応用問題A3⃣

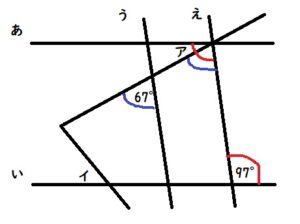
なので、アの角度は、97ー67＝30°です。

次にイの角度を求めます。

下図の赤線のように補助線を引くと、アと錯角の関係にある赤い角度はアと同じ30°です。

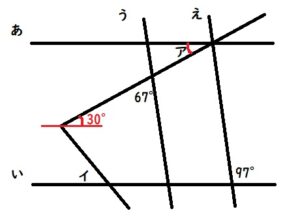
下図の青い部分は75°なので、

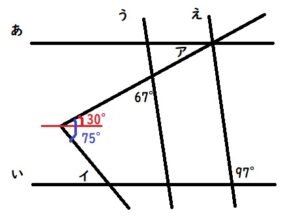
下図のように緑色の部分が75－30=45°と分かります。

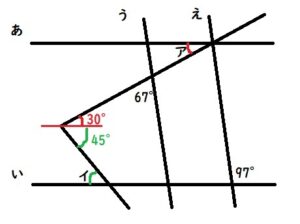
この45°とイは錯角の関係にあるので、イも45°です。

答え：ア＝30°、イ＝45°

応用問題A4⃣

下図の赤い角度は180－120＝60°

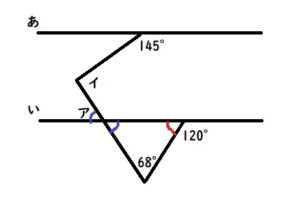
三角形の内角の和が180°ですから、青い角度は、

180－68－60＝52°

アは青い角度の対頂角なので52°となります。

次にイの所に下図の赤い補助線を引くと錯角が使えます。

緑色部分の角度は180－145＝35°です。

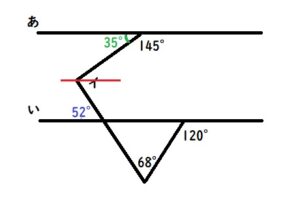
青の52°と緑の35°をそれぞれ錯角でイの所に持ってくると、

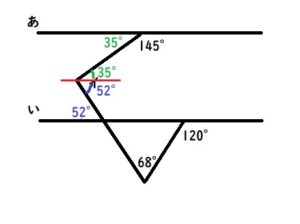
イの角度は35+52＝87°と分かります。

答え：ア＝52°、イ＝87°

応用問題B1⃣

赤い角度は360－335＝25°です。

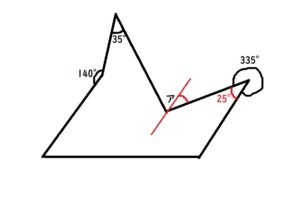
よって、錯角によりアの右半分も25°と分かります。

次に左側の平行線を、下の青線のようにのばします。

（このような線を延長線えんちょうせんと言います）

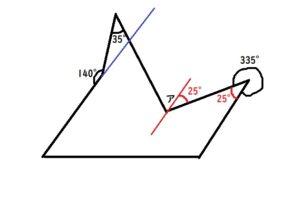
分かる角度を出していきます。

下図の青は180－40＝140°

緑は三角形の内角の和を利用して、180－35－40＝105°

紫は180－105＝75°です。

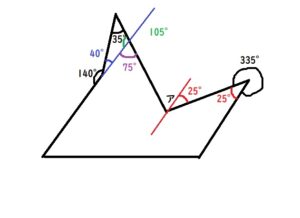
下図の紫の角度は錯角の関係にあるので、アの左半分は75となります。

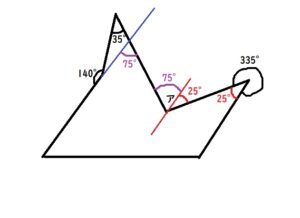
アの角度は、75+25＝100°となります。

答え：100°

応用問題B2⃣

下図のように2本の平行線あ・いがある場合、B＋C＝180°となります。これを利用します。

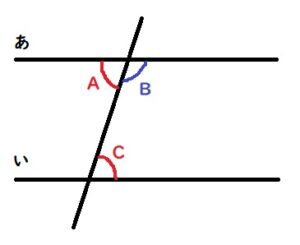
なぜ180°になるかというと、CはAの錯角であり、A＋B＝180°だからです。(AとBを合わせると直線になるので180°)

まず下図の赤線のように、平行線あ・いに平行な線を2本引きます。

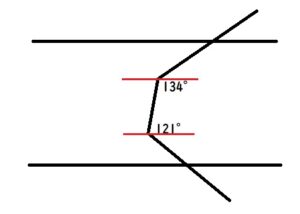
下図の赤い角度2個の合計は180°となります。（理由は上の赤い囲み枠をご覧ください）

よって青い角度2個の合計は、134＋121－180＝75°と分かります。

角度アと角度イの錯角を使うと、ア＋イ＝75°と分かります。

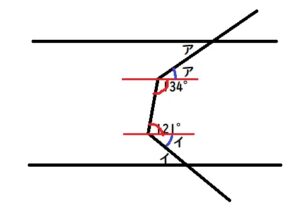
問題文よりイがアよりも15°大きいことを考えると、

ア＝30°、イ＝45°と分かります。

答え：30°