算オリの解答速報です!
最後に正答率調査をしていますので、ぜひご参加ください!
※公式解答速報と一致していることを確認しました
問題1
答え:2805264
2024=2×2×2×11×23なので、8、11、23で割って余りが出ないようにする。
- 8の倍数なので、下3ケタは224か264の二通り。
- 11の倍数なので、3つの□の合計は8か19のどちらか。(11の倍数の法則を使用)
仮に□に0を当てはめて23で割ると、2000224は19余り、2000264は0余る。1000が増えるごとに余りは11増え、100000が増えるごとに余りは19増えるので、つるかめ算的に残りの□が判明する。
問題2
答え:6985
<120>と<121>を比べると、<121>=11×11なので11が1個多く必要になる。同様に縦に比べていくと、125=5×5×5と127(素数)にも新要素があるのが分かる。
問題3
答え:(1)\frac{5}{8}(2)\frac{125}{576}
正方形AEFGを左にスライドさせると下図の図形ができるので、中央の正方形の面積は大きい正方形から直角三角形4個を引いて
1 – \frac{1}{4} × \frac{3}{4} ÷ 2 ×4 = \frac{5}{8}
問題4
(1)50通り (2)1925通り
※50個ある偶数番目マスのどこかで上に行く
問題5
答え:ア=41、イ=4649
12345679×9=111111111なので、星が4と分かる。
11111=4□×□□□から、11111=4□×2□□まで確定。
かけ算の答えの下1ケタが1になるのは、1×1、3×7、7×3、9×9のどれか。順番に試す。
1111111=□□□×4□4□についても、1111111=2□□×4□4□まで確定。
下1ケタを同様に試していく。
問題6
答え:26人
※6班と4班は下図のように24人までは重複せず、25人目で重複する。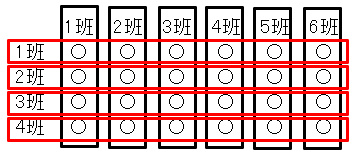
問題7
答え:256㎝²
三角形AMDを、Mを固定して反時計回転し、これを4つ合わせて40×40の巨大な正方形を作ると、中央に24×24の空白ができるから、求める面積は
((20+20)×(20+20)-24×24)÷4=256
問題8
答え:(1)048(2)601
3桁ごとに倍にしたものが並んでいくので、012,024,048,096…と並ぶ

コメント