2025年・第29回ジュニア算数オリンピック ファイナル解答速報!
2025年 第29回ジュニア算数オリンピックの解答速報です!
一番最後のアンケートにもぜひご参加ください!平均点と決勝ボーダーの予想に使わせていただきます。
問題1 (11点)
ア=5、イ=4、ウ=1、エ=6
問題2 (12点)
(1)21
(2)23
問題3 (13点)
18cm²
※7/21 12:41訂正しましたm(__)m
問題4 (14点)
A=8、B=9、C=7、D=496
問題5 (11点)
(1)イ→ア→ウ
(2)ウ→ア→エ→イ
問題6 (12点)
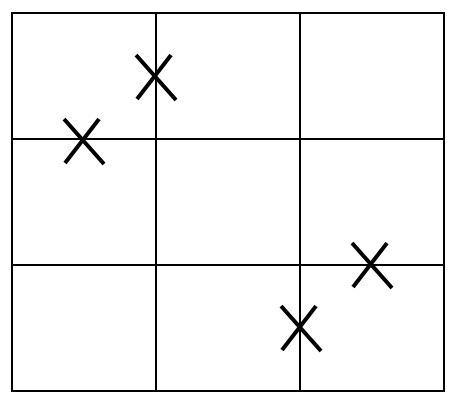
問題7 (13点)
(1)勝ち=Bさん、最後に宣言される数=1
(2)先手=Bさん、最初に宣言された数=9
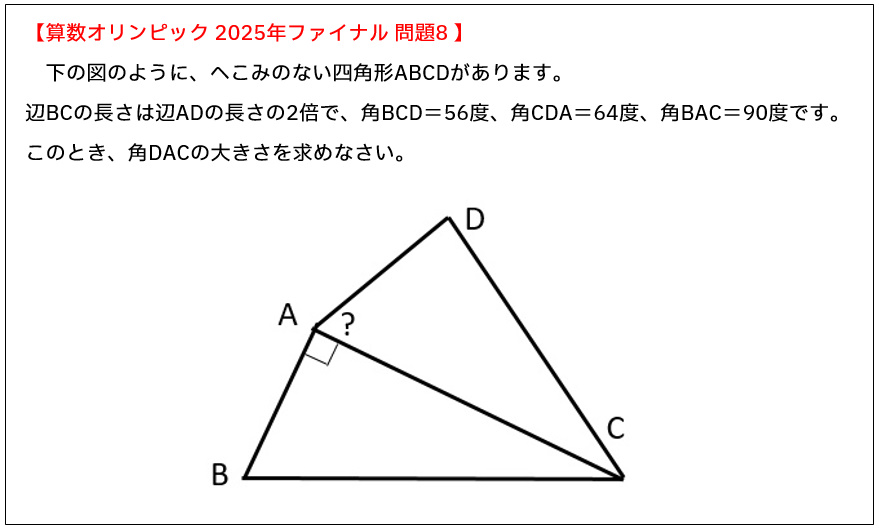
問題8 (14点)
51度
※7/21 18:30 この解答で間違いなさそうです。最初に出した解答から変更はありません
ご質問と回答
ご質問にここで回答します!
Q.問題1は6、5、2、8ではダメでしょうか? (①6✖️5=30、②2➕4=6、③9ー8=1) 問題8は54°にしたようです。
A.ダメだと思いますが、確かに問題文をよく見るときわどいですね。「0~9の数字が1つずつ入る」と書かれていますが、同じ数字は1回までと書かれていないと読めなくもないかも…。
Q.問題4、7.3.5.259だと間違いでしょうか?
A.間違いになると思います。7,3,5だと最小公倍数が105なので、259に+105するごとに他の答えが出て来るため、3桁の答えが259ただ1つになりません。
Q.(問題4) A8、B7、C9 D512 では、間違いでしょうか。 8、7、9の最小公倍数は504ですよね。
A.間違いになると思います。最小公倍数が504ということで、Dに入る数字が512だけでなく512-504=8もあり、答えが1つではなくなってしまいます。(問題文が分かりにくいですが、あくまで「1~999の中で」1つかどうかという問題です)
2025ジュニア算オリ正解率調査!
正解した問題を全て教えてください。正解率調査と決勝ボーダー予想の参考にさせていただきます!


コメント
問題4に関して質問させてください。
————–
Q.(問題1) A8、B7、C9 D512 では、間違いでしょうか。 8、7、9の最小公倍数は504ですよね。
A.間違いになると思います。最小公倍数が504ということで、Dに入る数字が512だけでなく512-504=8もあり、答えが1つではなくなってしまいます。
————–
とありますが、D=8は3桁の整数ではないので除外になりませんか?
よろしくお願いいたします。
>匿名さん
ああ…これは確かに問題文が分かりにくいですね!
元の文章が「1から999までのAの倍数で~となるのはDだけです」なので、1から999までの間に答えが2つがあってはだめなんです。
もしも「1から999までのAの倍数で~となる3桁の整数はDだけです」という問題だったら、ご指摘の通り、8はカウントされないので512も正解になります。
これは問題文がもうちょっとわかりやすく書かれているとありがたいですよね。ご指摘ありがとうございました。