2022年ジュニア算オリファイナル問題1

次の筆算が成り立つ数字の組み合わせは何通りありますか。
ただし、それぞれの数の一番大きい位に0は入らないものとします。
解答・解説
下図の赤背景のマスに何の数字が入るか、1から順に考えていきます。
まずは1から。
赤背景が1の時
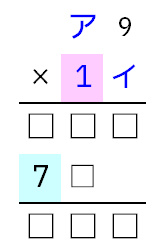
この時、アに7を入れると水色背景のマスが7になります。
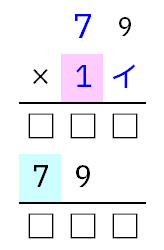
イに入れる数字は、1だと答えが3桁にならないので失敗です。
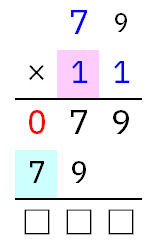
しかし3以上を入れると、今度は最終的な計算結果が4桁になってしまうので失敗します。
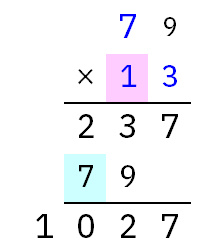
つまりイに入るのは2のみです。
赤背景が1の時は、「79×12」の1通りが成り立ちます。
赤背景が2の時
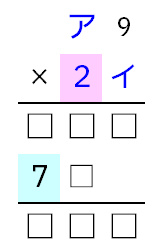
赤背景が2の時は、アに3を入れると水色背景が7になります。
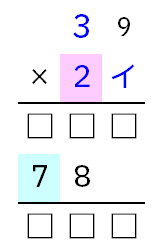
この時イには、1や2を入れると答えが3桁になりません。
また、6以上を入れると最終結果が4桁になってしまいます。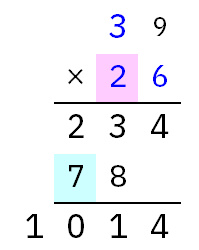
よって、イに入るのは3,4,5の3通り。
つまり、赤背景が2の時は、「39×23」「39×24」「39×25」の3通りが成り立ちます。
赤背景が3の時
赤背景が3の時は、アに何を入れても、水色背景が7になってくれません。
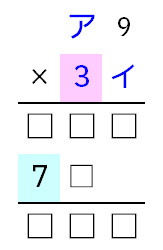
よって、赤背景が3の時に成立する式は0通りです。
赤背景が4の時
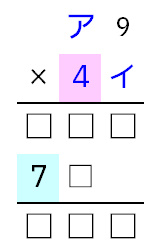
赤背景が4の時は、アに1を入れると水色背景が7になります。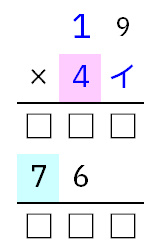
この時イに入る数字が5以下だと、かけ算の結果が3桁になってくれません。
6以上ならOKです。今回は最大の9を入れても、最終結果は3ケタに収まります。
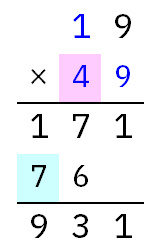
よって、赤背景が4の時に成立する式は「19×46」「19×47」「19×48」「19×49」の4通りです。
赤背景が5以上の時
赤背景が5以上の時は、アに何を入れても、水色背景が7になってくれません。
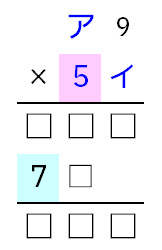
よって、赤背景が5以上の時に成立する式は0通りです。
以上をまとめて、全部で1+3+4=8通りとなります。
答え:8通り


コメント