【ジュニア算オリ】2022年問題9 解答・解説 / ジュニア算数オリンピック

ジュニア算数オリンピック 2022年問題9

下の図の四角形ABCDの面積を求めなさい。ただし、ACの長さはCDの長さの2倍です。

まず下記のように補助線を引き、底辺の長さが同じ三角形を作ります。

すると下図の赤線の長さは同じなので、

3cm×8cmの三角形を下にもう1個くっつけることができます。

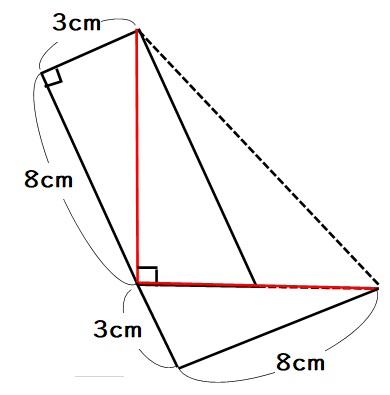
この台形の面積は、（上底＋下底）×高さ÷2の式に当てはめると

$（3＋8）×11÷2=60.5cm^{2}$

この台形の中身は、下図のように紫2個とピンク2個に分けられます。（色が同じ三角形は面積も同じ）

求めたい面積は紫1個＋ピンク1個ですから、台形全体の半分となります。

$60.5÷2=30.25cm^{2}$

答え：30.25cm²

中学で習う「三平方の定理」を知っていれば簡単に解けます。

$AB^2+BC^2=AC^2　より$

$64+9=AC^2$

$AC=\sqrt{73}$

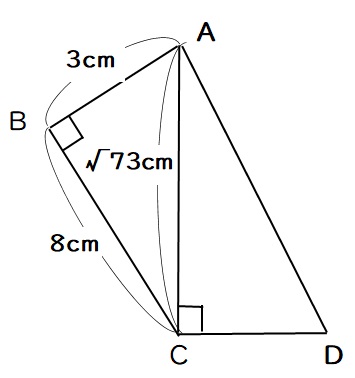
CDはACの半分なので、

$CD=\frac{\sqrt{73}}{2}$

△ABCの面積は

$AB×BC÷2$

$=3×8÷2$

$=12cm^2$

△ACDの面積は

$AC×CD÷2$

$=\sqrt{73}×\frac{\sqrt{73}}{2}÷2$

$=\frac{73}{4}$

$=18.25cm^2$

求める面積は△ABCと△ACDの合計なので、

$12cm^2+18.25cm^2=30.25cm^2$

答え：30.25cm²