2022年ジュニア算オリファイナル問題4

連続する4つの1以上の整数について、それらの平方数(同じ整数を2回かけ合わせたもの)の和をAとします。
例えば、連続する4つの整数が8,9,10,11のとき
8×8+9×9+10×10+11×11=366
となるので、Aは366になります。
Aが、3で割ると2余り、5で割り切れる4桁の整数になるとき、連続する4つの整数として考えられる組み合わせを2つ答えなさい。
解答・解説
問題文の2つの条件「3で割ると2余る」「5で割り切れる」について、順番に見ていきます。なお、連続する4つの整数の先頭をXとします。
Aを3で割ると2余る
例えば8の平方数というのは、半径8の正方形の面積と同じです。
つまり、連続する4つの整数の先頭をXとすれば、平方数は下図のような4つの正方形の面積と同じです。
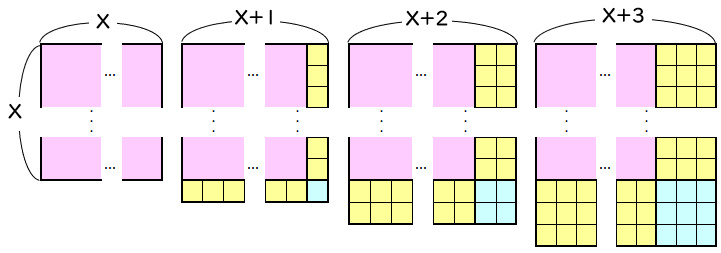
この4つの正方形の面積の合計について考えてみます。
黄色の部分を数えると、全部でX個が12列ぶんあります。
青色の部分は全部で14マスあります。
問題文より、赤と黄色と青の合計が3で割ると2余ることが分かっています。
青は3で割ると2余り、黄色は3で割り切れるので、赤色の部分も3で割り切れることが分かります。
赤色部分が3で割り切れるということは、つまり、Xは3の倍数です。
Aが5で割り切れる
Aが5で割り切れるということは、Aの1の位は5か0です。
ところで、ある整数が1,2,3,4…と増えると、その平方数の1の位は
1,4,9,6,5,6,9,4,1,0…と、この10個を繰り返していきます。
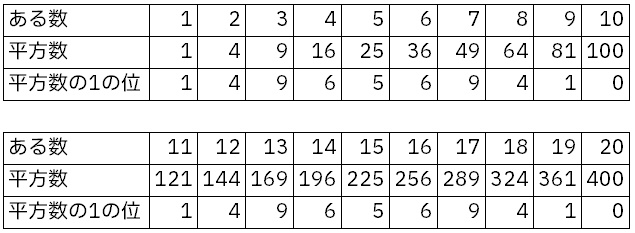
この中の連続する4つを選んで5で割りきれるのは、
- 1+4+9+6=20
- 6+9+4+1=20
のどちらかのみです。
つまり、連続する4つの整数は「●1、●2、●3、●4」か「●6、●7、●8、●9」のどちらかです。
よって、連続する4つの整数の先頭の数Xは1の位が1か6です。
条件を満たす組み合わせを求める
以上より、2つの条件が分かりました。
- Xは3の倍数
- Xは1の位が1か6
これらを満たすXは、小さい方から順に、6、21、36、51、66…となります。
X=6の時、
A=6×6+7×7+8×8+9×9=230で、4桁という条件を満たしません。
X=21の時、
A=21×21+22×22+23×23+24×24=2030で、これは全ての条件を満たします。
X=36の時、
A=36×36+37×37+38×38+39×39=5630で、これは全ての条件を満たします。
(X=51以上の時は、Aが5桁以上になってしまうため条件を満たしません)
以上より、考えられる組み合わせは
「21,22,23,24」と「36,37,38,39」となります。
答え:「21,22,23,24」と「36,37,38,39」

コメント