2022年ジュニア算オリファイナル問題8

解答・解説
まず左上のマスから順番に考えてみます。
最初の1マス目は、何を入れても良いので、3通りの色が考えられます。

次にその右隣のマスを考えます。ここは左のマス以外の色なら良いので2通りです。

次にその右、その右…と考えていくと、どれも隣と同じじゃなければよいので、2通りです。
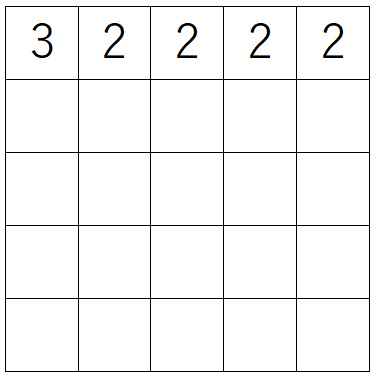
次に左上から、一番左の列を下に向かって考えていきます。
ここもやはり「上と同じでなければよい」ので、2通りです。

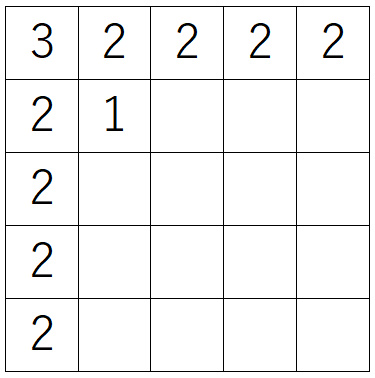
次に、左から2番目・上から2番目のマスについて考えます。
ここでは、下図の2マス×2マスの赤枠に注目。

ここまでの間に、この赤枠の中には、右下以外には数字が入っています。その数字の入り方は、以下の2パターンのどちらかです。

つまり、2種類の色が入っているか(上図左)、3種類の色が入っているか(上図右)のどちらかです。
上図左の場合、この4マスで3種類の色を入れないといけないので、まだ使っていない色を入れるしかありません。使える色は1通りです。
上図右の場合、左隣とも上隣とも違う色を入れないといけないので、使える色は1通りです。
つまり、どちらにしろ1通りしか選ぶことができません。
さて、ある2マス×2マスのうち3マスが埋まっていたら、残りの1マスは1通りしか色が選べないことが分かりました。
では次に、その隣の2マス×2マスを見てみましょう。
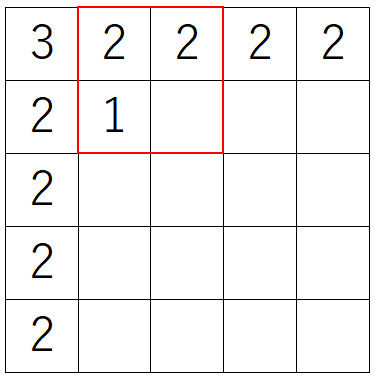
残ったマスに使える色はやはり1通りしかありません。
このように考えていくと、残りのマスはすべて1通りしか色が選べないことが分かります。
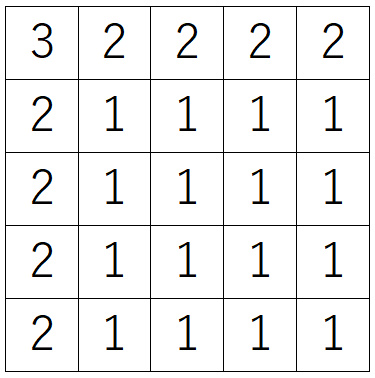
よって、全部の塗り方は、
$$3×2×2×2×2×2×2×2×2=768通り$$
答え:768通り

コメント