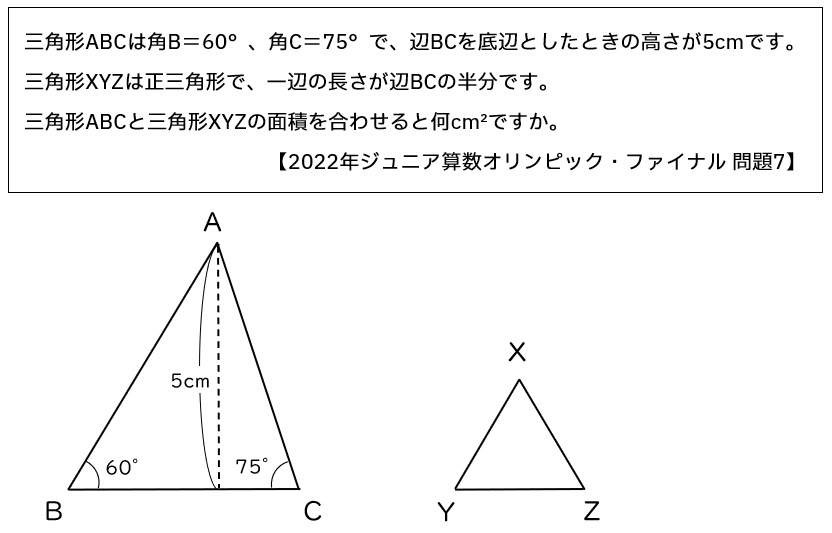
2022年ジュニア算オリファイナル問題7
解答・解説
もっと楽なやり方があるかもしれません。見つけたらぜひコメントで教えてください!
まず同じ図形をもう1つくっつけてみます。
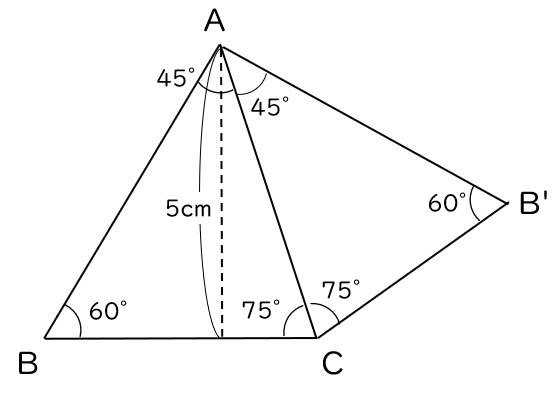
そしてBCとAB’の交点をDとします。
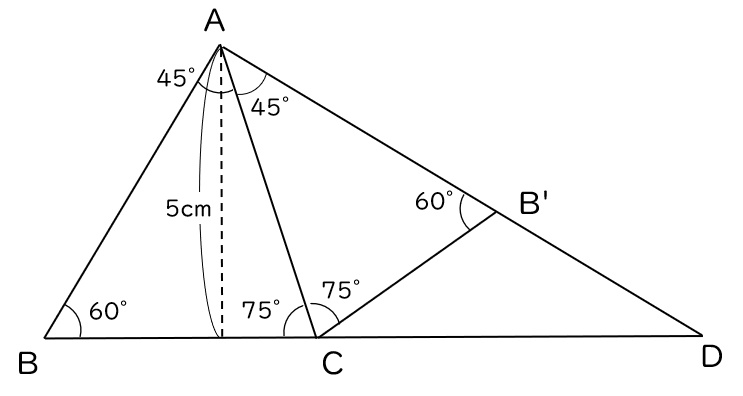
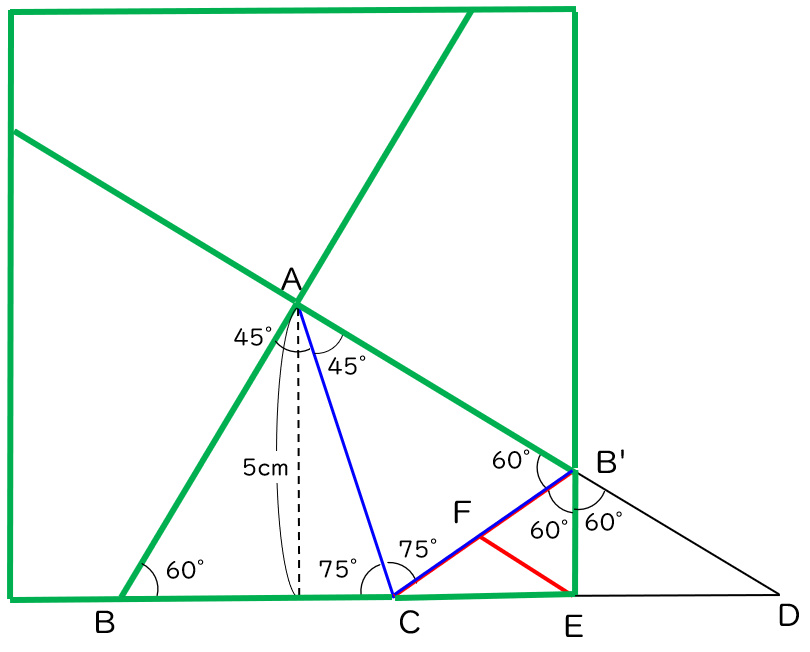
B’から垂直に補助線を下ろし、BDとの交点をEとします。
B’Eは三角形B’CDをちょうど2等分する線なので、角CB’Eと角DB’Eはどちらも60°です(下図)
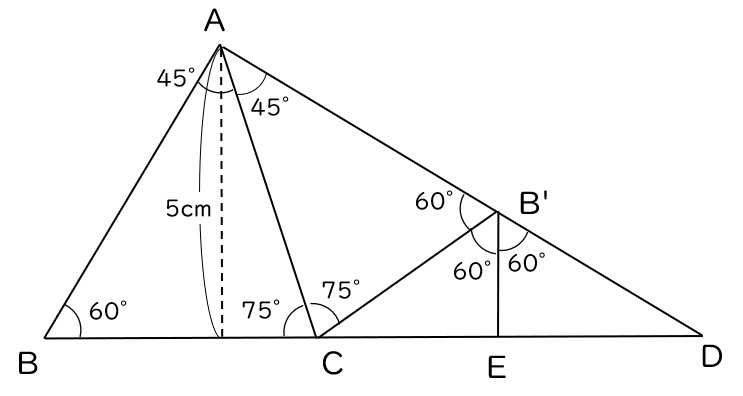
また、三角形CB’Eは30°60度90度の直角三角形なので、B’Eの長さはB’Cの半分です。
さらにB’Cの中点をFとすると、
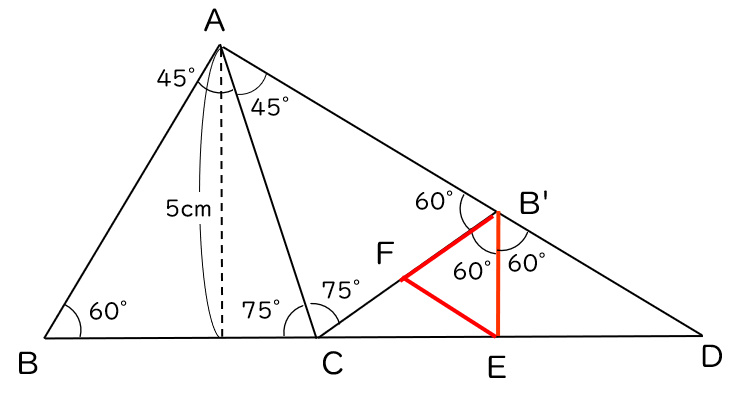
B’EとB’FはどちらもB’Cの半分の長さなので、上図の赤い三角形が正三角形だと分かります。
この正三角形は、問題文の正三角形XYZと同じ大きさです。
また、下図の2つの赤い三角形は面積が同じです。(底辺B’FとFCの長さが同じで、高さが同じため)
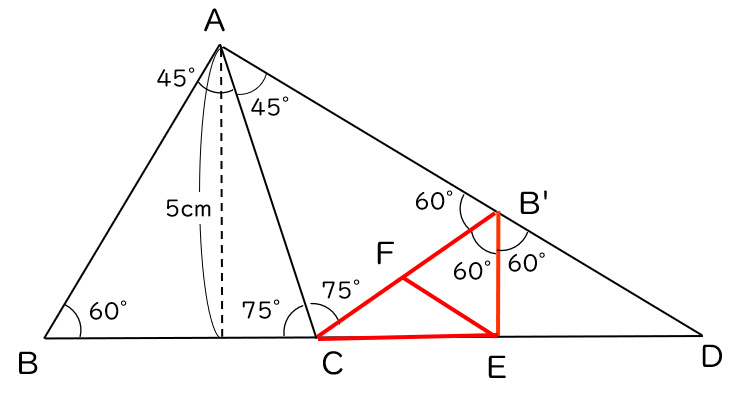
求めたい面積は、下図の青線の三角形と赤線の三角形の合計です。
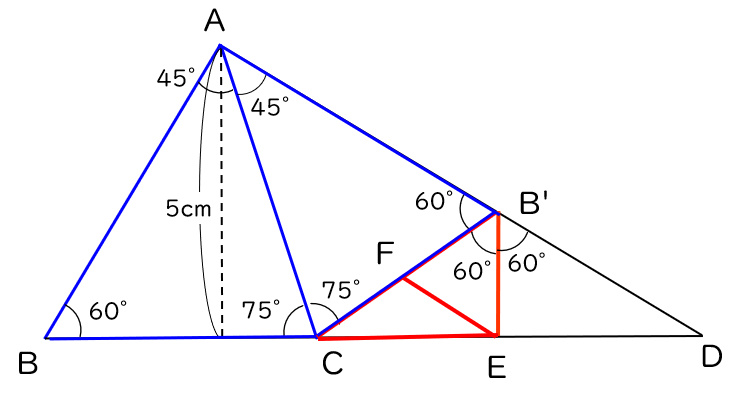
つまり、これらを緑枠で囲んでできる下図の四角形は、求めたい面積の2倍となります。
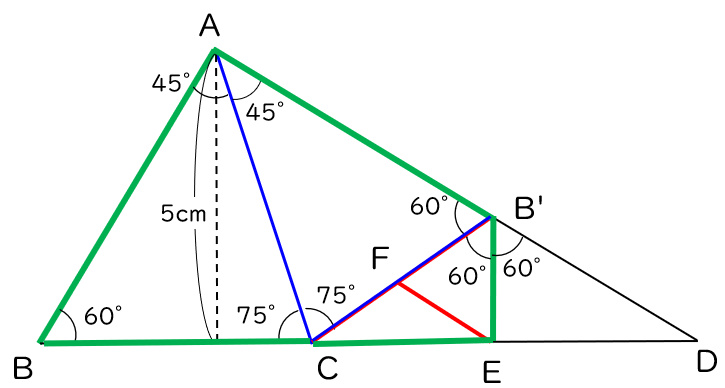
この緑枠の四角形は、下図のように4個くっつけると大きな正方形になります。
この大きな正方形は1辺の長さが10なので、面積は
$$10×10=100cm²$$
つまり緑枠の四角形1個の面積は
$$100÷4=25cm²$$
緑枠の四角形は求めたい面積の2倍でしたから、
求めたい面積は
$$25÷2=12.5cm²$$
答え:12.5cm²


コメント