算数オリンピック トライアルの問題感想
2024年6月16日(日)に開催された算数オリンピック・トライアルの問題の個人的な感想を述べます。


まず問題1は算オリではおなじみの、3桁×2桁の虫食いかけ算。難度も抑えめで、取れた子が多そうですが、理詰めしようとするとやや解きにくい問題でした。
問題2は頭を使って解く問題。適当にやっても全ての答えが出ない(出た答えが全てかどうか自信が持てない)ので、落ち着いて論理的に答えることが重要そうです。Aが3桁であることに気づけば、落ち着いて過不足なく答えられたと思います。
算オリもジュニア同様、問題3・問題6・問題9が図形問題でした。問題3は易しめ…というかほぼ中学受験の常識で解ける問題。問題6も中学受験っぽさのある問題で、問題9は算オリらしい閃きを必要とする難問でした。問題6・問題9は出来の差が大きかったのではないでしょうか。
問題4はキッズBEE・ジュニア算オリにも類題が出たカードの問題で、それらよりはやや難し目。過去に似た出題が少なく、前提知識よりもその場での思考が必要な問題でした。とりあえず数字が「023456」だと分かったら、後は6の裏が0と仮定して、ダメなら2と仮定して…と気合でやれば解けます。理詰めよりこの方が早かった子も多いかもしれません。
問題5は素数に関する問題で、素数の中には偶数が1つ(2)しかないというのが出発点となっていました。その後は理論と気合で解いていきます。
問題6は前述のとおり図形問題ですが、やや中学受験のテクニック寄りな印象。一見典型問題に見えるだけに、逆に閃きが必要な部分が思いつきにくかったかもしれません。
問題7は連続する数の和に関する知識を結び合わせるとすぐ答えが出る問題。ちなみに算オリが出版する「明日への算数」第4問「連続する数の和」に似た問題がありました。
問題8はAさんとBさんとCさんが何試合もやって合計の得点を競うという、キッズBEEやジュニア算オリによく出る問題。ただ計算すると引き分けの回数が異常に多い結果になるので、自信を持って計算できないと見返す羽目になりそうです。
問題9は算オリっぽさのある図形問題。過去問で色々詳しくなっていると、最後に見たことのある図形(15度・75度・90度の直角三角形)が出てきて、面積を求めることができます。
問題10は場合の数の難問ですが、気合いで全通り数えるという力技では答えにたどり着くことは難しい一方で、ちゃんと理解していれば理詰めで解ける良問でした。欲を言えば(1)が勘で書くとそこそこの確率で当たってしまうのが難点でしょうか。
各問題の正解率と平均点予想
アンケートを基に算出した各問題の予想正解率は下表の通りです。
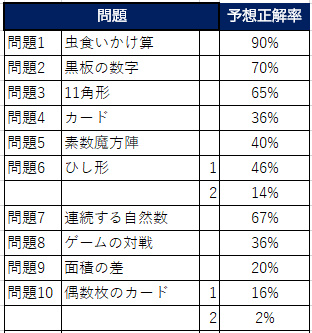
全体を通してみると、問題6(2)と問題10が難しく、問題4・5・6(1)・8・9あたりが出来の分かれそうな問題だったようです。
閃きやテクニックで解ける問題のうちいくつかは、気合いで大量の計算や数え上げを行うことで解くこともできたりしますが、全部気合いで解くには時間が足りなかったと思われます。
平均点は45~55点、ファイナル進出ボーダーは60~70点程度かなと思っています。
平均点と決勝進出ボーダーの算出根拠
例年同様、皆さんからのアンケートを基に、補正をした正解率を使っています。

また決勝ボーダーは、予選参加人数・決勝進出人数が去年と同じと仮定し、過去の平均点と決勝ボーダーの関係から予想しています。

コメント
おてう様
今年も参考にさせていただきました。
ジュニア算数でトライアル無事に通過できました。
我が息子は4年生です。
ファイナルはレベルが高そうなのでメダルまでたどり着けるか・・・。
昨年同様、大阪会場へ出陣予定です。
おめでとうございます!
算オリのメダルは問題運も大きいので難しいですね。頑張ってください!