ジュニア算数オリンピック 2022年問題10
1、2、3…97、98、99のように、1から99までの数が表に書かれたカードが1枚ずつあります。この99枚のカードの裏にも数が書かれており、表と裏に書かれた数の和はどのカードも100になっています。
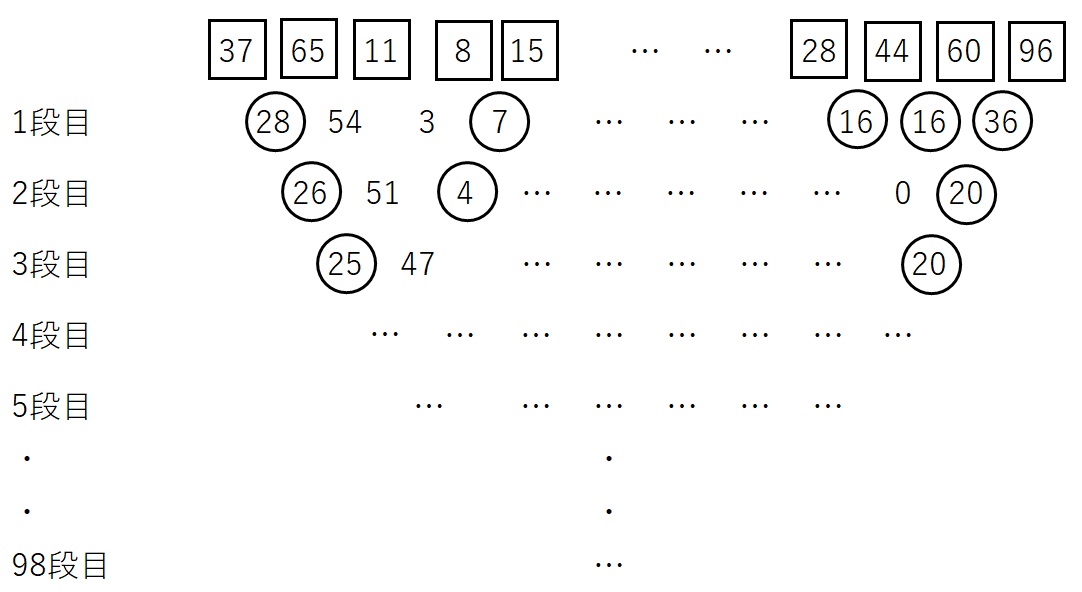
このカードを表向きにして下の図のように一列に並べ、隣り合った数の差を1段目、2段目、…と次々に書いていきます。
差を書くときに、「右上の数-左上の数」で差を求めたときは、その差に○をつけます。「左上の数-右上の数」で差を求めたときや差が0になるときは、その差や0に〇はつけません。
いま、カードをすべて表向きに一列に並べて差を書いていくと、1段目から98段目までに○がついた数が全部で1625個ありました。次に、カードの並びはかえずにすべて裏向きにして差を書いていくと、○がついた数が全部で1613個になりました。
カードがすべて表向きに並んでいたときに2段目から98段目までに○がついた数は何個ありましたか。
答え
「全て表向きの時」の1段目と、「全て裏向きの時」の1段目を比べると、
〇の付いていた数字に〇が付かなくなり、○の付いていなかった数字に〇が付くことになります。
1段目に書かれる数字自体は同じです。
そのため、2段目以降に書かれる文字や○のあるなしは、「全て表向きの時」と「全て裏向きの時」で全く同じになります。
つまり、1625個と1613個の違いというのは、1段目の違いです。
全て表向きの時の1段目の98個の数字は、〇付きが55個、○なしが43個と分かります。
$$(98+12)÷2=55$$
$$55-12=43$$
よって、全て表向きの時の2段目から98段目までに○が付いた数は、
$$1625-55=1570$$
答え:1570個



コメント