2022年ジュニア算オリファイナル問題2

1、2、3、…、20の数が書かれたカードが1枚ずつ、合計20枚あります。これをAさん、Bさん、Cさん、Dさんの4人に5枚ずつ配ったところ、以下のようになりました。
・Aさんのカードに書かれている数の合計は、Bさんのちょうど3倍です
・Cさんのカードに書かれている数の合計は、Dさんのちょうど2倍です
・Aさんは「3」のカードを持っています
このとき、Dさんの持っているカードに書かれている2番目に大きな数は何ですか。
解答・解説
AさんはBさんの3倍なので、AさんとBさんの合計は4の倍数になります。
CさんはDさんの2倍なので、CさんとDさんの合計は3の倍数になります。
また、4人の合計は1~20の合計なので、
$$(1+20)×20÷2=210$$
となります。
これらの条件から、まずはBの持つ5枚の合計とDの持つ5枚の合計としてありえる数字を書き出してみます。
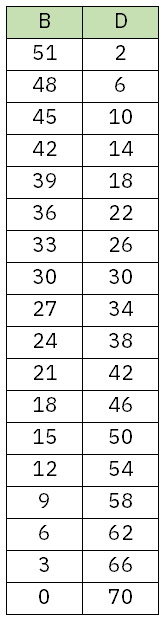
Aが3を持っているため、Bの合計は最も小さい時でも18となります(1,2,4,5,6の時)。17以下とはなりません。
また、BとDの持つ10枚の合計は、最も小さい時でも63となります(1,2,4,5,6,7,8,9,10,11)。62以下とはなりません。
上の表に対して、これらの条件を満たさないものに灰色を付けると、下表のようになります。
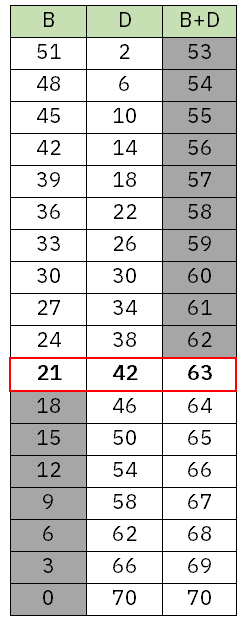
つまり条件を満たすのは、Bの合計が21、Dの合計が42、BとDの合計が63の時のみとなります。
先ほど書いた通り、BとDの合計が63ということは、その10枚とは1,2,4,5,6,7,8,9,10,11です。10と11は、BかDのどちらかが持っています。
しかし、Bの5枚の合計は21なので、5枚の組み合わせは(1,2,4,5,9)(1,2,4,6,8)(1,2,5,6,7)のどれかとなります。Bは10や11は絶対に持っていません。
つまり、10と11は絶対にDが持っていることが分かります。
Dは12以上は持っていないので、Dの一番大きな数は11、2番目に大きな数は10となります。
答え:10

コメント