低学年特有の「パズルのような算数問題」は解かせるべきかどうか

パズルのような算数問題

最近、小学校低学年向けの難問として、パズルのような算数の問題が増えてきています。

算数オリンピックの低学年版であるキッズBEEや、大手中学受験塾のテストなどでも、算数と言うよりパズルに近いような問題がよく出題されます。

パズルのような算数問題とは？

パズルのような算数の問題とは何かというと、いろんなものがあるので一言では言えないのですが、例えばこんな問題です。適当に3問作ってみました。

下図のようなサイコロを、手前に2回、右に2回転がしたら一番上の目は何になるでしょう？

（注：図から奥に1回倒すと一番上の目は2になります。図から右に1回倒すと一番上の目は3になります）

はじめて見る人は、「えっ、これ算数なの・・？」って思うかもしれません。

このくらいの難度ならまだ解けるかもしれませんが、ちょっと難しくすると子供たちは大混乱。このような問題をやったことがある子とない子で結構な差がついてしまいます。

ただ中学受験では、こういったパズル問題が出題されることはあまりなく、「ニュートン算」「差集め算」「旅人算」のようないわゆる特殊算と呼ばれる問題や、平面図形・立体図形などの問題が多く出題されます。

だから、低学年のうちに算数パズル問題を解く意味は、中学受験する上ではあんまりないのでは？と思われている方もかなり多いのではないかと思います。

順番を逆に

僕は、「算数対策で子供にパズル問題を解かせる」という順番でパズルを始めるのはあまりよくないと考えています。

そもそも、パズルのような問題を見れば、知的好奇心のある子供はたいてい興味を持ちます。それはおもちゃやテレビゲームに興味を持つのと似たような感覚です。

そうなると、別にテスト対策でパズルをやるわけではなく、単にパズルが楽しいからパズルをやるというだけの話になります。

で、そのパズルがたまたま算数の役にも立って、良かったね、という感じになるのが個人的な理想です。

子供が自分から好んでパズルを解く場合、子供の中ではパズルを解く時間が遊びの時間に分類されます。逆にパズルを親から「やらされている」ものだと思われてしまうと、子供にとってはパズルと勉強の合計時間が拘束時間であると感じてしまうことになります。この差は大きいです。

雑に図示してみるとこんな感じです。

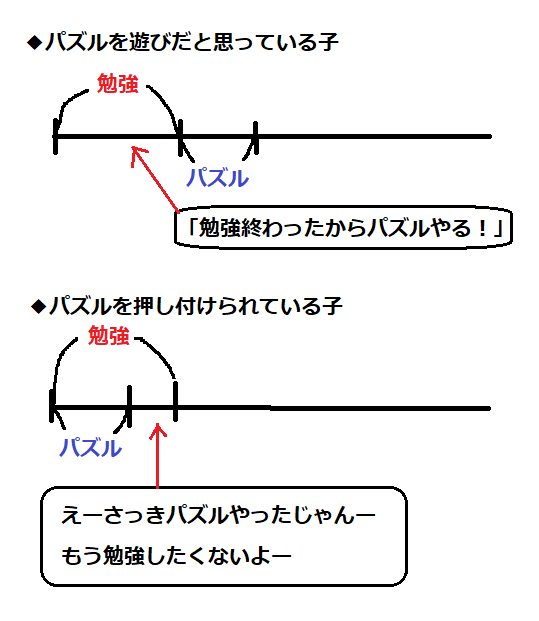
勉強とパズルの関係（あくまでイメージです）

子供によって面白いパズルと面白くないパズルが違いますので、子供が気に入るパズルが見つかるまで色々見せてみるのが良いと思います。

その結果、全く解かれず無駄になってしまった本もいくつかありますが（例えば数独は興味ありませんでした…）、押し付けないことが大事で、子供が自分の意思でパズルをやっている（と子供に思ってもらう）ことが大事と考えています。

おまけ：問題の答え

答え：Aさんが3位、Bさんが2位、Cさんが1位

解説：Bさんは偶数なので2位しかありません。AさんとCさんのどちらかが1位でどちらかが3位になりますが、CさんがAさんに勝っているので、Cさんが1位となります。

答え：122

解説：3つだけなので全て書き出しましょう。一番小さいのは102、次が120、3番目がが122です。

下図のようなサイコロを、手前に2回倒し、右に2回倒したら、一番上の目は何になるでしょう？

答え：６

解説：サイコロは2回倒すと裏になるので、どっち側に倒そうとも2回倒せば6の裏側になり（6の裏側は1ですが）、もう2回倒せばまた裏になって6に戻ります。