2020年数オリンピック・キッズBEE解答速報!
2020年のキッズBEEお疲れさまでした!
ここで出す解答は筆者が独自に作成したものです。また、問題文も大幅に省略しています。かなり雑に作っていますのでご了承ください。難度や正解率も個人の予想です。以上ご了承ください。
問題や解答の公表は6月17日まで不可とのことで、本記事は6月18日に公開しました。なお、正式な解答は6月23日に公式さんのほうで出るようです。
2020年キッズBEE講評
2020年のキッズBEEは自宅受験となりました。試験時間も90分と普段のキッズBEEより長く、問題数も多かったため、どの子も苦労したのではないでしょうか。
問題が多かった理由ですが、おそらくトライアル(予選)とファイナル(決勝)の問題が両方詰め込まれていたのだと思います。全11問のうち、おそらく6番か7番までがトライアルで出題する予定の問題で、それ以降がファイナルの問題だったのではないでしょうか。2020年のキッズBEEは、難問が後半に固まっていました。
2020年のキッズBEE平均点は40点程度ではないかと思います。ただ、自宅受験は通常の試験より点数が上がる傾向があるようなので、その点を加味してどうなるかは分かりません。
ではここから、2020年のキッズBEE問題と解答の一覧です!
2020年キッズBEE第1問
0~9の数字を1回ずつ使って足し算を完成させます(146は使用済み)。アの位置に入る数字は?
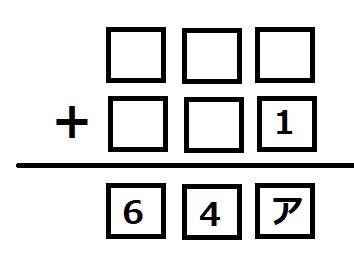
第1問解答
8
※難度:易 予想正解率:80%程度
百の位に注目。答えが6になっていますが、1+5や2+4をしようにも、1や4がすでに使われているので使えません。
したがってここには2+3が入ります。
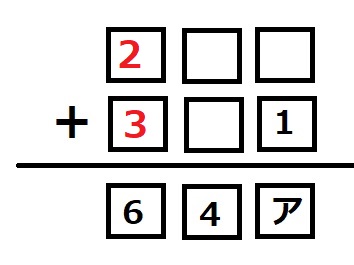
次に十の位に注目。残りは5,7,8,9ですが、この中で足して4になるのは5+9のみ。
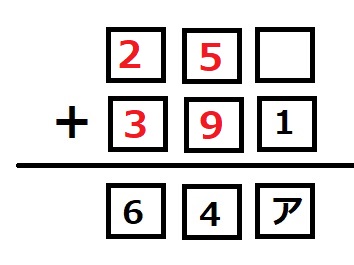
最後に残った7と8を1の位に入れるので、アの位置には8が入ります。
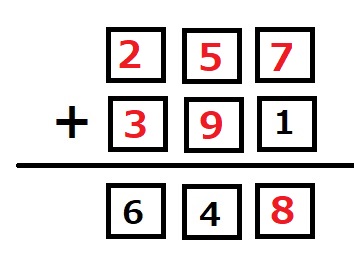
2020年キッズBEE第2問
32人の生徒のうち何人かが右手、何人かが左手を挙げ、何人かは手を挙げていません。
最初上がっている手の本数は19本でしたが、先生が「右手を挙げていない人は右手を挙げてください」と言うと、上がっている手の本数は39本になりました。
(1)初めに手を挙げていなかったのは何人?
(2)初めに左手だけを挙げていたのは何人?
第2問解答
【とい1】13人 【とい2】7人
※難度:やや易 予想正解率:50%程度
「右手だけ」「左手だけ」「全く挙げていない」の3つに分けて考えます。
最初手は19本挙がっていたので、手を全く挙げていなかったのは13人です。次に、手の上がっている本数が19本から39本に増えたので、右手を挙げていなかったのは20人です。
- 「全く挙げてない」=13人
- 「左手だけ」+「全く挙げてない」=20人
従って、左手だけ挙げていたのは7人です。
2020年キッズBEE第3問
0~9までの数字を入れて、上の数字が下の2つのレンガの数字の間の数字になるようにしなさい。
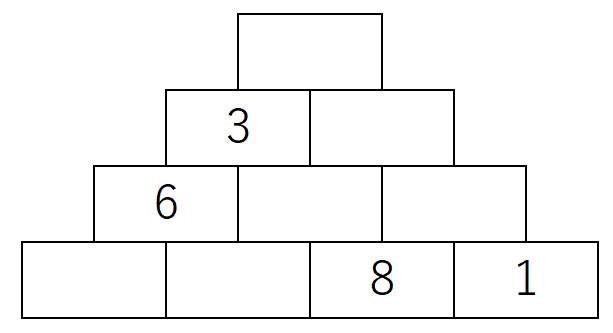
第3問解答
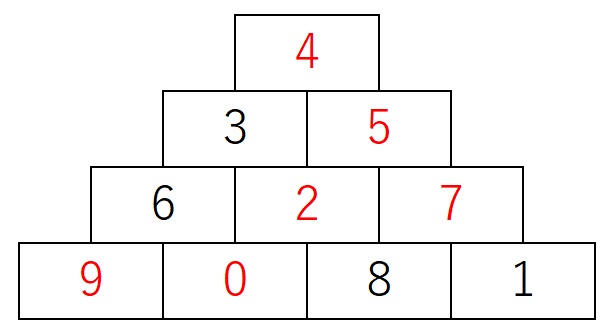
※難度:やや易 予想正解率:70%程度
最大値である9と最小値である0は、一番下段にしか入ることができません。
また、8の隣に9を入れてしまうと、8と9の上に入れられる数字がありません。
従って最下段は左から順に9,0,8,1となります。
次に3に注目。6の右のマスには3より小さい数が入る必要がありますが、もう0と1が使われているので2を入れるしかありません。
残りは4,5,7ですが、7は、8か9の上にしか置けません。そのため二段目右端が7に決まります。残りは三段目に5、四段目に4です。
2020年キッズBEE第4問
図のAからBまで時計回りに測ると20cmでした。この形の周りの長さは?
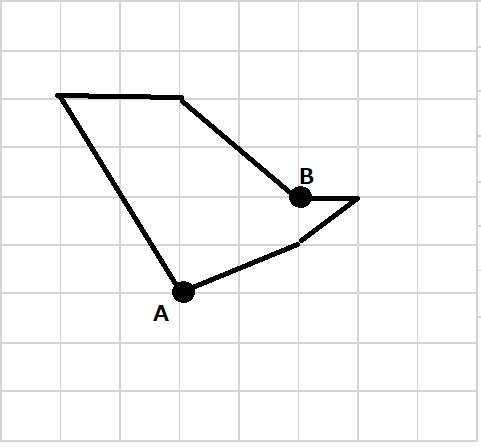
第4問解答
30cm
※難度:やや易 予想正解率:60%程度
AからBまでの部分と、BからAまでの部分を、それぞれ3つに分けます。
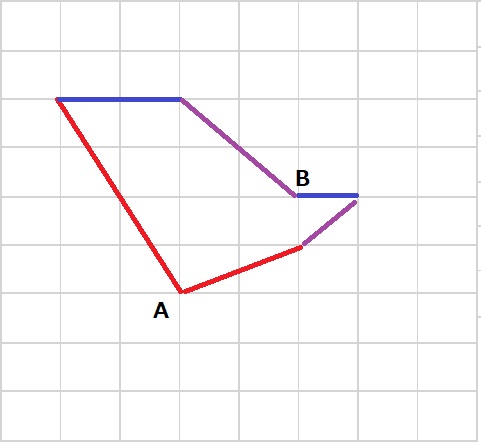
上の図の同じ色の部分を見比べると、それぞれ2倍になっています。
従ってBからAまでの長さは、AからBまでの長さの半分です。周りの長さの合計は、20cm+10cm=30cmとなります。
2020年キッズBEE第5問
1cm x 1cm x 1cmの積み木を9個組み合わせて図のような大きな箱の形を作りました。上から見た時、面は次のうちどのように見えますか。1~4から選びなさい(選択肢省略)
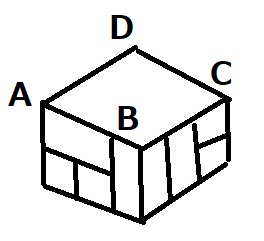
第5問解答
1
※難度:やや易 予想正解率:70%程度
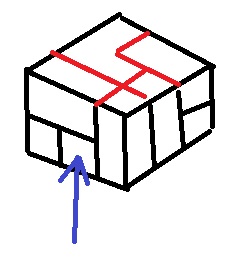
まず目に見えている部分を書くだけで(赤線)、すぐに1か4に絞れます。

ABの間の下段の積み木(青矢印)に注目すると、4ではないことが分かります。
2020年キッズBEE第6問
4つの袋に玉が何個かずつ入っています。どの3つの袋を合計しても31個以上になるとき、4つの袋の玉の合計は最も少ない場合で何個ですか。
第6問解答
42個
※難度:普通 予想正解率:50%程度
4個の袋の中身がなるべく均等なほうが、合計は少なくなります。なぜなら、1つの袋だけ極端にたくさん入っていても、結局それ以外の3つの袋で合計31個入っていないといけないので、1つの袋に極端にたくさん入っていると意味がないばかりか4袋合計の玉の数は増えてしまうためです。
平均的に入れる場合、31個の玉は3個の袋に11個、10個、10個に分けることになります。残りの1個の袋は10個では足りません。それだと選び方次第で10個、10個、10個の袋が選ばれて合計30個になってしまうためです。最後の1個の袋も11個入っている必要があるので、答えは11+10+10+11=42個となります。
2020年キッズBEE第7問
2桁の数の十の位と一の位で足し算と掛け算をした時、掛け算の答えより足し算の答えが大きくなるような、2桁の数は全部で何個?(例えば13は1×3より1+3の方が大きいので題意を満たす)
第7問解答
26個
※難度:普通 予想正解率:40%程度
掛け算より足し算が大きくなるのは、0か1を含むときのみ。
従って10~19の10個と、20,30,40…90の8個と、21,31,41…91の8個が該当します。
個数は10+8+8=26個となります。
2020年キッズBEE第8問
Aさん、Bさん、Cさんの3人がグラウンドを3周する競争をしました。
- 1周目にスタート地点を通った時、一番早かった人は18秒、次が20秒、次が22秒でしちゃ
- 2周目にスタート地点を通ったのも同じように2秒ずつの違いがありました。また、2周目だけにかかった時間も2秒ずつの違いがありました。
- 3人とも1周目より2周目、2周目より3週目の方が時間がかかりましたが、1周に30秒以上かかった人はいませんでした。
- 1位はCさんで、2位はBさんでその1秒後、3位はさらにその1秒後にゴールしました。
- Cさんは1周に1秒ずつ遅くなっていきました。
Aさんが3周目にかかった時間は何秒?
第8問解答
28秒
※難度:難 予想正解率:10%程度
2周目で題意を満たす組み合わせを考えます。次の(1)(2)2通りが考えられます。
(1)
- 1周目18秒の人→2周目(x+4)秒 ※合計x+22秒
- 1周目20秒の人→2周目(x)秒 ※合計x+20秒
- 1周目22秒の人→2周目(x+2)秒 ※合計x+24秒
(2)
- 1周目18秒の人→2周目(x+2)秒 ※合計x+20秒
- 1周目20秒の人→2周目(x+4)秒 ※合計x+24秒
- 1周目22秒の人→2周目(x)秒 ※合計x+22秒
(1)(2)それぞれについて、3人のうちどれがCさんか考えてみます。
まず(2)では、1周目18秒の人がCさんなら、2周目は19秒のはずです。しかしそれだと1周目22秒の人が2周目を17秒で走ったことになり、1周目より早いので題意に反します。
1周目20秒の人がCさんなら、2周目は21秒ということになりますが、これもやはり1周目22秒の人が2周目を17秒で走ることになり題意に反します。
ということで、1周目22秒の人がCさんで、x=23です。
- 1周目18秒の人→2周目25秒 ※合計43秒
- 1周目20秒の人→2周目27秒 ※合計47秒
- 1周目22秒の人→2周目23秒 ※合計45秒
Cさんは3周目さらに1秒遅かったので、3周目は24秒となります。つまりCさんは、合計69秒で1位だったことになります。
題意より2位は70秒、3位は71秒でゴールしたことになります。ところが、1種目20秒の人が2周目27秒なので、3周目は28秒以上かかることになり、合計で75秒以上となってしまいます。(2)は矛盾が生じてしまいました。
残った(1)について、同様にCが誰か推理していくと、下記のようになります。
- 1周目18秒の人→2周目25秒 ※合計43秒
- 1周目20秒の人→2周目21秒 ※合計41秒
- 1周目22秒の人→2周目23秒 ※合計45秒 ←Cさん
従って(1)では矛盾は生じず、Cさんは3周目24秒、合計69秒で1位ゴールとなります。
つまり2位は70秒、3位は71秒です。
次に2周目を終えて41秒になっている人を考えます。誰も1周30秒には達していないので、2周目を終えて41秒の人が3周目を終えて71秒だったということはあり得ません。3周目は29秒で合計70秒だったことが分かります。2位のBさんです。
残った人が3位のAさんで71秒ですから、1周目18秒→2周目25秒→3周目28秒だったことがわかります。
2020年キッズBEE第9問
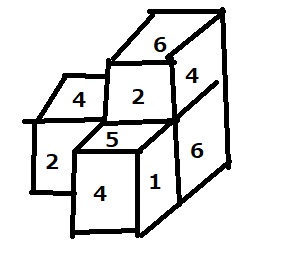
図のようなサイコロが4個ある。
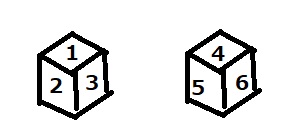
サイコロ4つを図のように机の上に積みました。
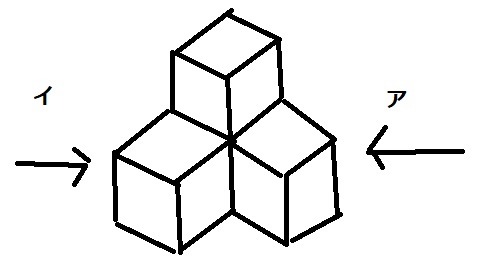
アの向きから見ると下図のように見えた。イから見える9つの数字の合計は?
第9問解答
大きい数:45 小さい数:42
※難度:やや難 予想正解率:30%程度
イから見える中で分かる部分を全部書くと合計40となります。イから見た下段左奥の1マスのみ分かりません。
しかしこのマスは1と6は入らないので、最小で42、最大で45となります。
2020年キッズBEE第10問
1~5の数字が書かれたカードが1枚ずつあります。カードの重さは1g、2g、3g、4g、5gのどれかで、同じ重さのカードはありません。カードに書かれた数字と重さの数字が同じものは1枚だけです。
これらを図のように3回天秤に乗せるとすべて釣り合いました。
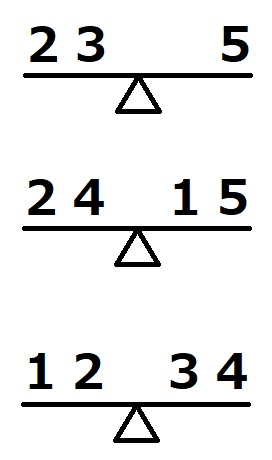
それぞれのカードの重さは何gですか。
第10問解答
1=4g、2=2g、3=1g、4=5g、5=3g
※難度:やや難 予想正解率:20%程度
5つのカードのうち4つのカードが乗った天秤に注目。左の2枚と右の2枚の重さが同じということは、これら4枚の重さの合計は偶数となります。1~5までの合計は15で奇数ですから、4つのカードに使われていない最後の1枚が奇数であることが分かります。
つまり、3と5が奇数です。
1番の天秤より、2が奇数であることが分かります。
これで既に2と3と5に関しては下記のどれかしか可能性はありません。
- 2=2g、3=1g、5=3g (1)
- 2=2g、3=3g、5=5g →番号と重さが一致してるカードが1枚じゃないのでダメ
- 2=4g、3=1g、5=5g (2)
可能性の残った(1)と(2)について、残りの1と4の重さを考えてみます。
(1)
- 2=2g、3=1g、5=3g、1=4g、4=5g ←OK
- 2=2g、3=1g、5=3g、1=5g、4=4g ←2と4が番号と重さ一致 ×
(2)
- 2=4g、3=1g、5=5g、1=2g、4=3g ←天秤が釣り合わない ×
- 2=4g、3=1g、5=5g、1=3g、4=2g ←天秤が釣り合わない ×
ということで、答えは2=2g、3=1g、5=3g、1=4g、4=5g です。
2020年キッズBEE第11問
1~50のカードから6枚取ったら、0~9の数字が1回ずつ使われていました。
(1)6枚のカードの合計は最大でいくつ?
(2)6枚のカードの合計は最小でいくつ?
(2)6枚のカードの合計は何通り考えられる?
第11問解答
【とい1】171 【とい2】135 【とい3】5通り
※難度:やや難 予想正解率:20%程度
6枚のカードに0~9の合計10個の数字が書いてあったので、6枚のカードの数字は2桁が4枚と1桁が2枚です。
これら6枚のカードの数字を足し算する筆算を考えてみましょう。
・○○
・○○
・○○
・○○
・・○
+・○
ーーー
○○○
十の位に4つ、一の位に6つの数字が入ります。
カードは50までしかないので、十の位に入る数字は、1~5のどれかです。
合計を最大にするには十の位を最大にすればいいので、十の位にできるだけ大きい数字(5,4,3,2)を入れ、一の位に残りの0,1,6,7,8,9を入れると、最大値が171となります。
最小値は同様に、十の位にできるだけ小さい数字(1,2,3,4)を入れ、一の位に残りの0,5,6,7,8,9を入れると、最小値は135となります。
合計は何種類かというと、十の位に1~5のうち何を入れるか考えてみればわかります。
先ほど最大値の時は5432を入れる(つまり1を入れない)、最小値の時は1234を入れる(つまり5を入れない)としました。他に2を入れない、3を入れない、4を入れない、が可能なので、合計値は実は5種類しかないことが分かります。


コメント