低学年で数検を受ける方へのアドバイス
子供が小2で数検準2級(高1)、小3で数検2級(高2)に合格しました。

その経験から、低学年で数検を受ける方へのアドバイス的なことを書いてみたいと思います!
5級と準2級の壁
数検は5級から以下のような大きな違いがあります。
- 算数検定から数学検定に名前が変わる(中学生以降の範囲になる)
- 一次試験と二次試験があり、試験時間が長い
- 範囲が増え、問題の難度自体も上がる
- 論述が増えてくる
特に中学範囲に入る5級と、高校範囲に入る準2級に、大きな壁があります。
算数検定から中学検定へ
数検は5級から「数学検定」と名前を変え、試験範囲が小学生の範囲を出て中学・高校へと移ります。そのため、数検5級以降で学ぶことはあまり中学受験の役には立たないです。
「中学受験のためになるかどうか」で判断する人にとっては、数検5級以降は意味がない試験ということになり、あくまで子供が興味を示した場合にのみオススメという感じになります。
なお準2級からは高校の範囲になります。
試験時間が長い
数検5級~3級は、一次試験(50分・30問)と二次試験(60分・20問)という2つのテストを受けることになります。
さらに、数検準2級以降は二次試験が90分になります。
算国理社ではなく数学だけでこの時間ですから、低学年では集中力が持たなくなる子も多いと思います。
一次だけでも受かれば次回は一次が免除で二次だけ受けることになるので、2回受けて合格するようなプランもアリだと思います。ちなみに難しいのは二次の方です。
範囲が増え、問題の難度が上がる
数検は級が進むにつれて範囲が広くなり、問題も難しくなる(基本さえ知っていれば解ける問題は減り、頭を使って解く問題が増えてくる)ため、合格率も下がっていきます。特に準2級から顕著です。
数検6級までは合格率80~90%程度ですが、
中学範囲の5級~3級では合格率60~70%程度に下がり、
高校範囲の準2級以降は合格率30~40%程度に下がります。
例えば2級の場合、範囲はこんなにあります。
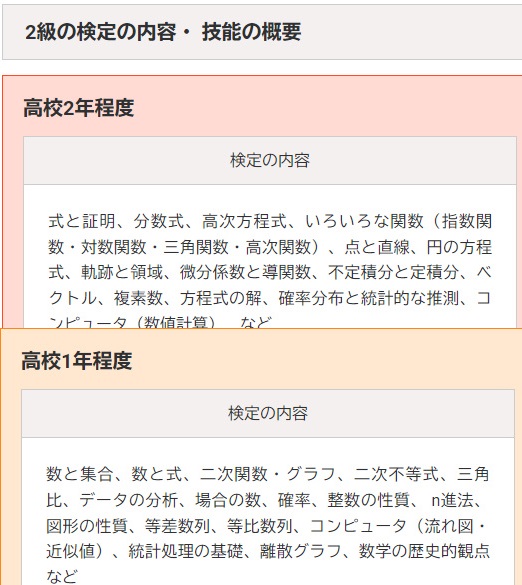
▲数検2級の範囲はこれ全部
3級までは基本問題が多く、算数の延長という感もあるので、まだ楽しく学びながら取れると思います。
難度に関しては、ざっくりのイメージではこんな感じです。
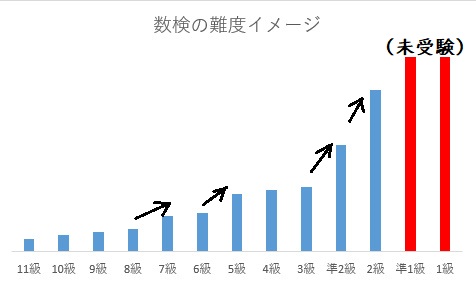
記述問題が増えてくる
記述問題では、答えだけでなく、答えに至るまでの式や考えなどを書く必要があります。
記述問題は5級から出てきます。
5級~3級では記述問題は2問程度ですし、書く内容も短く簡単(普段問題用紙に書いていることを書けば良い)なので、低学年でも対応可能です。

▲3級までは数行で済む記述が多い
ただ準2級以降は、二次試験のほぼ全問で記述が必要になります。
記述する内容も膨大になり、ちゃんとした説明が求められます。
まだ日本語を上手く使えない低学年では、この記述が大きな壁となりやすいと思います。
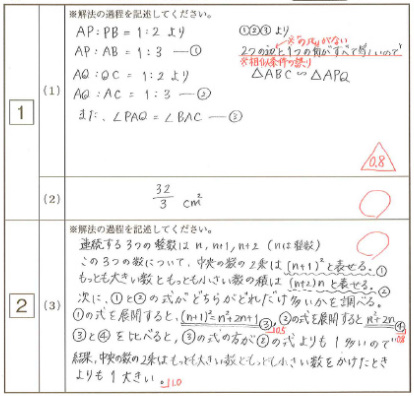
▲文章が必要になり、厳密性も問われる
(以上、数検公式サイトより一部抜粋)

まとめ
5級~3級は、数学に興味のある子なら結構いけると思います。数検自体も良い教材なので、チャレンジしてみると良いです。
ただ、算数好きな子は「答えだけ出せば満足」という子も多いはずです。準2級(高1)からは記述の存在が重くなるので、算数・数学が好きだからと言って、数検にチャレンジするのが良いとは限らないと思います。
また後に行くほど難しくなり、分量も増えるので、小4以降で中学受験塾に通いながら数検5級(中学範囲)以降にチャレンジするのは慎重に考えたほうが良いと思います。
数検は中学受験で有利?
なお、中学以降の算数を知っていると中学受験算数で有利になる問題もたまに存在しますが、数検程度の簡単な問題を解けても、問題文に対して方程式を使いこなせるレベルには達しない、という点にも注意が必要です。
こちらの記事もご覧ください。


コメント