2022年キッズBEEファイナル問題7
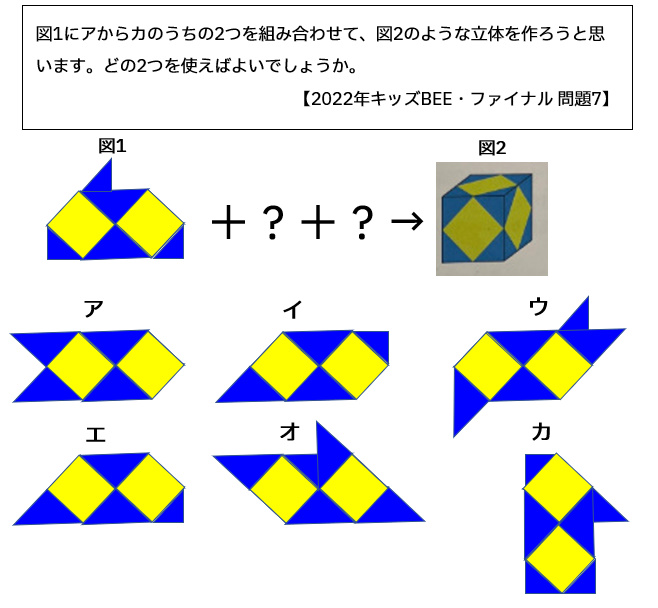
図1にアからカのうちの2つを組み合わせて、図2のような立体を作ろうと思います。どの2つを使えばよいでしょうか。
解答・解説
まず図1は、立体の2面分の面積より小さな三角形1個分だけ欠けた形です。
この状態を「-1」と呼ぶことにします。
同じルールでア~カの面積を調べると、
ア=±0、イ=-1、ウ=+1、
エ=-1、オ=+1、カ=±0
と表すことができます。
図1とあと2つ合わせて立体の6面ぶんの面積になるためには、±0のもの1つと、+1のもの1つを選べばよいことがわかります。
次に、青い▲は3つ集まって1つの角になることに注目します。
±0のものはアかカのどちらかですが、アは青い▲2つのペアが4カ所にあります。青い▲は3つ集まるはずなので、これら4カ所すべてにあと青い▲が1つずつ付く必要がありますが、ウにもオにもそのような青い▲はありません。そのため、アではなくカが正解だと分かります。
図1とカと、もう1つはウとオのどちらかになります。
後は実際に図1、カをそれぞれ折り曲げた図を描いてみて、ウとオのうち当てはまるものを選ぶと良いでしょう。
答え:オとカ


コメント